Skip to contents

Great-circle Segment Between Two Vectors

Source: R/stereonet_base.R
stereo_segment.Rd

Plots the great-circle segment between two vectors

Usage

stereo_segment(
  x,
  y,
  upper.hem = FALSE,
  earea = TRUE,
  n = 100L,
  BALL.radius = 1,
  ...
)

Arguments

x, y

objects of class "Vec3", "Line", "Ray", or "Plane"

upper.hem

logical. Whether the projection is shown for upper hemisphere (TRUE) or lower hemisphere (FALSE, the default).

earea

logical TRUE for Lambert equal-area projection (also "Schmidt net"; the default), or FALSE for meridional stereographic projection (also "Wulff net" or "Stereonet").

n

integer. number of points along great-circle (100 by default)

BALL.radius

numeric size of sphere

...

optional graphical parameters passed to graphics::lines()

See also

slerp(), stereo_greatcircle, stereo_lines()

Other stereo-plot: fault-plot, lines.spherical(), plot-spherical, points.spherical(), stereo_arrows(), stereo_cones, stereo_confidence(), stereo_contour, stereo_lines(), stereo_point(), stereoplot(), stereoplot_guides(), stereoplot_ticks(), text.spherical()

Examples

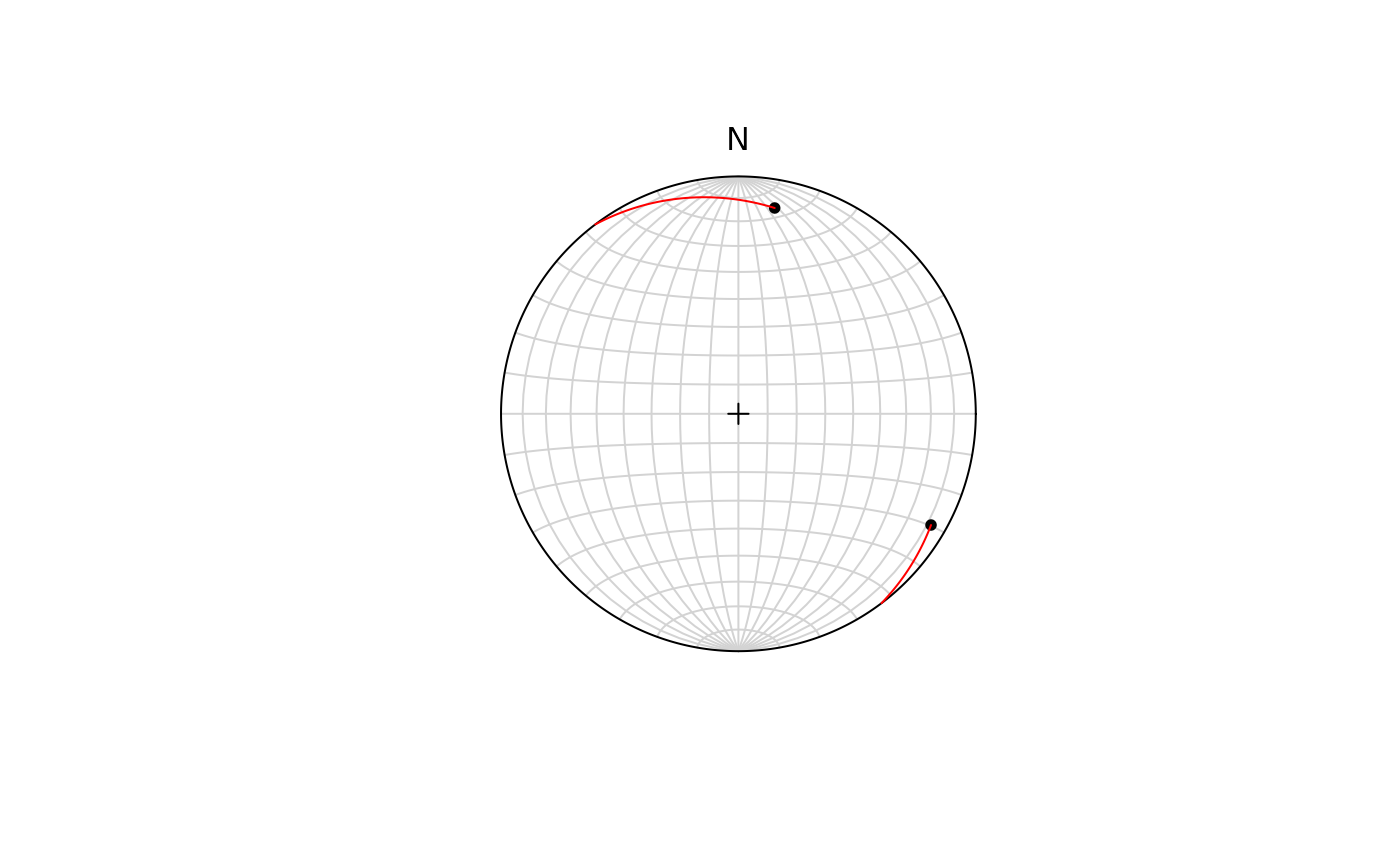
x <- Line(120, 7)
y <- Line(10, 13)
plot(rbind(x, y))
stereo_segment(x, y, col = "red")


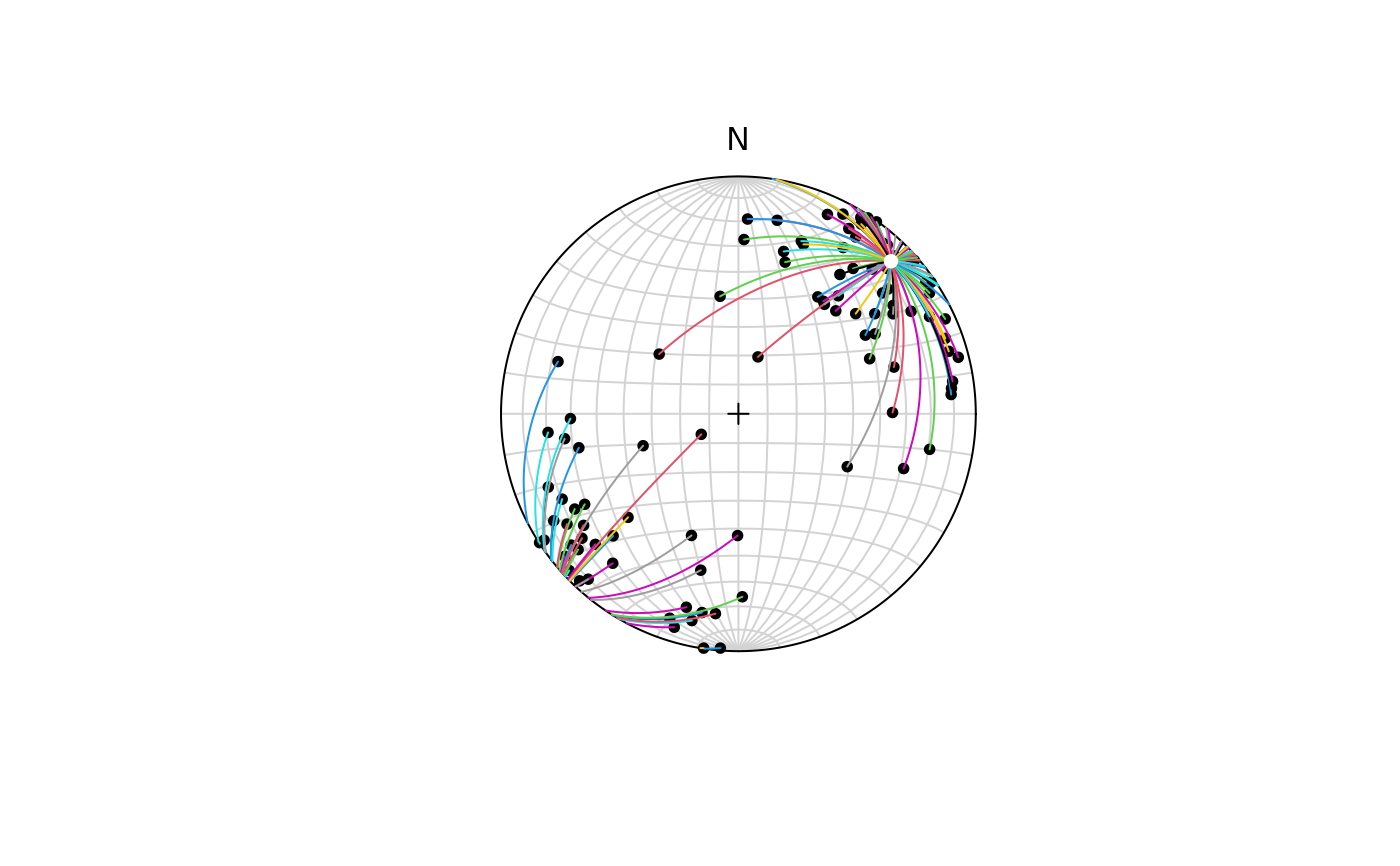
# For multiple segments use lapply():
set.seed(20250411)
mu <- Line(45, 10)
x <- rvmf(100, mu = mu)
plot(x)
invisible(lapply(seq_len(nrow(x)), FUN = function(i) {
  stereo_segment(x[i, ], mu, col = i)
}))
points(mu, pch = 16, col = "white")