Spherical Linear Interpolation (Slerp)

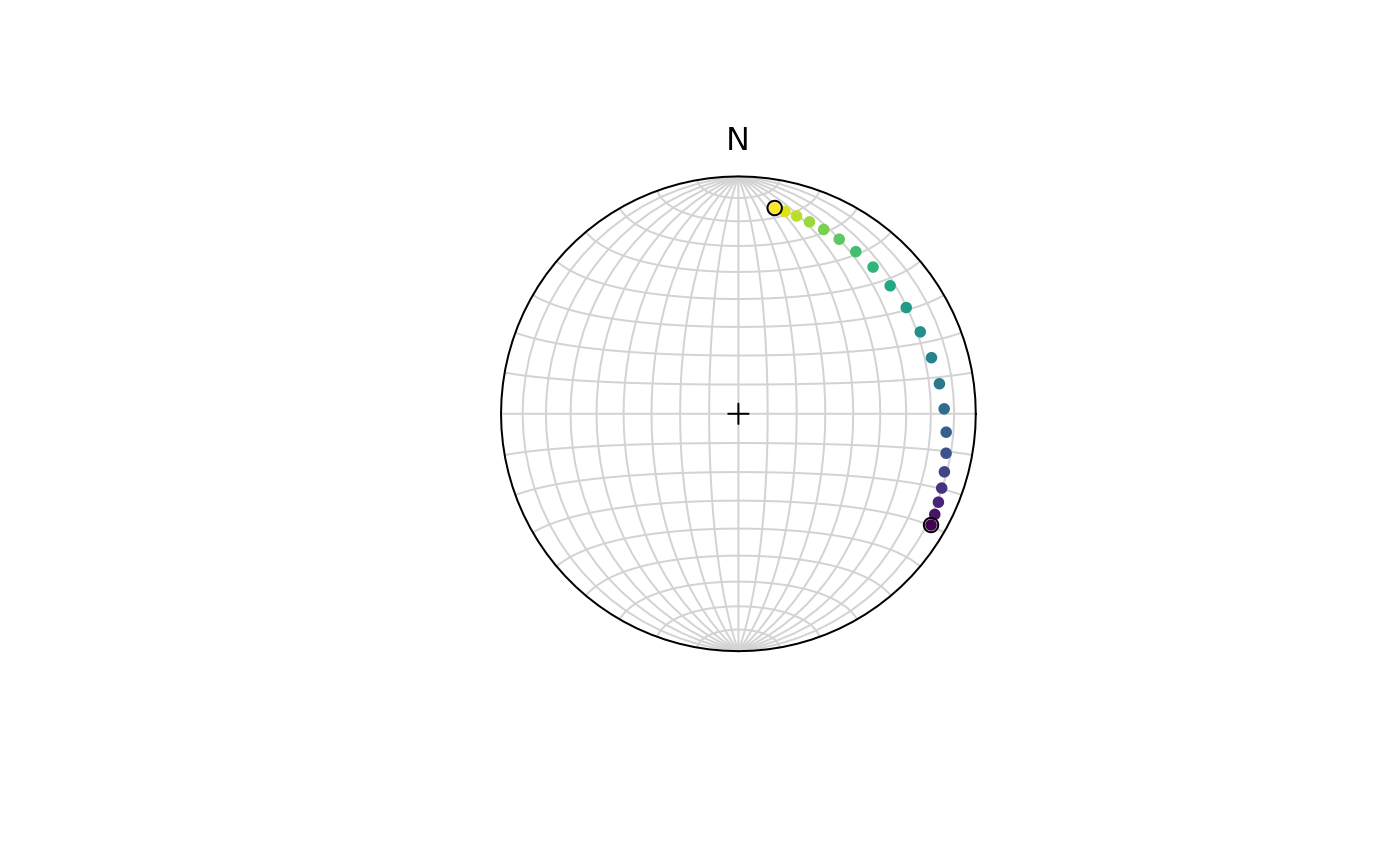
Returns the spherical linear interpolation of points between two vectors

Usage

slerp(x0, x1, t)

# Default S3 method
slerp(x0, x1, t)

# S3 method for class 'Vec3'
slerp(x0, x1, t)

# S3 method for class 'Line'
slerp(x0, x1, t)

# S3 method for class 'Ray'
slerp(x0, x1, t)

# S3 method for class 'Plane'
slerp(x0, x1, t)

# S3 method for class 'Pair'
slerp(x0, x1, t)

Arguments

x0, x1

objects of class "Vec3", "Line", "Ray", or "Plane" for the first and the last points of the to be interpolated arc.

t

numeric. Interpolation factor(s) (t = [0, 1]).

Value

object of class x0

Details

A Slerp path is the spherical geometry equivalent of a path along a line segment in the plane; a great circle is a spherical geodesic. The Slerp formula is derived from the spherical law of sines. The formula for Slerp between two unit vectors x0 and x1 is: $$\text{Slerp}(x_0, x_1; t) = \frac{sin((1 - t) \theta)}{sin(\theta)} x_0 + \frac{sin(t \theta)}{sin(\theta)} x_1$$ where the angle \(\theta\) is the angle between x0 and x1, and t is the interpolation factor (ranging from 0 to 1), i.e. the fraction along the geodesic path between x0 and x1 for which interpolated vector will be calculated.

Note

For non-unit vectors the interpolation is not uniform.

See also

stereo_segment() for plotting the Slerp path as a line

Examples

x0 <- Line(120, 7)
x1 <- Line(10, 13)
t <- seq(0, 1, .05)
xslerp <- slerp(x0, x1, t)

plot(xslerp, col = assign_col(t))
points(rbind(x0, x1))