Statistics on the Sphere

This tutorial describes how to calculate basic statistics for spherical orientation data using the structr package. It covers the calculation of mean orientations, dispersion measures, hypothesis testing, orientation tensors, and clustering of orientation data.

Load the package:

library(structr)

To start, we import some example planes and lines, and convert them to spherical objects:

data(example_planes_df)
data(example_lines_df)

planes <- Plane(example_planes_df$dipdir, example_planes_df$dip)
lines <- Line(example_lines_df$trend, example_lines_df$plunge)

Mean and dispersion

Arithmetic mean, geodesic mean, and projected mean

Arithmetic mean and variance

The arithmetic mean orientation of spherical data is calculated by summing up all orientation vectors and normalizing the resulting vector¹:

This involves the resultant vector of a set of $n$ vectors $x_1, \ldots, x_n$ , given by $\bar{\mathbf{x}} = \sum_{i=1}^{n} \mathbf{x}_i$ , and the resultant length defined as $\bar{\mathbf{R}} = \sqrt{x_x^2 + x_y^2 + x_z^2}$ .

The arithmetic mean of the vector components is the mean resultant vector, i.e the resultant vector normalized by its length $\mu = \frac{\bar{\mathbf{x}}}{\bar{\mathbf{R}}}$

In geology, the statistical estimators are useful for vectorial data ("Line" objects) such as lineations (e.g. mineral lineations, stretching lineations) or plunge directions of fold axes, but less for axial data ("Ray" objects) such as paleomagnetic directions or orientations of fold axes, where the direction is not relevant².

These estimators are good descriptors of the concentration of the data around the mean direction, assuming an unimodal, isotropic distributions such as the von Mises-Fisher distribution.

Define some weights for our lines based on the quality reported for the measurements:

example_lines_df$quality <- ifelse(is.na(example_lines_df$quality), 6, example_lines_df$quality) # replacing NA values with 6
line_weightings <- 6 / example_lines_df$quality

The (weighted) arithmetic mean orientation of spherical data is:

lines_mean <- sph_mean(lines, w = line_weightings)

… and the (weighted) arithmetic variance

lines_variance <- sph_var(lines, w = line_weightings)

the (weighted) standard deviation (i.e. the 63% cone around the mean) and the 95% confidence cone around the mean:

lines_delta <- delta(lines, w = line_weightings)
lines_confangle <- sph_confidence_angle(lines, w = line_weightings)

Taken together, this prints as

c(
  "Variance" = lines_variance,
  "63% cone" = lines_delta,
  "Confidence angle" = lines_confangle
)
#>         Variance         63% cone Confidence angle 
#>        0.1938084       36.2745102        6.9017035

Summary stats can also be retrieved through

summary(lines)
#>         azimuth          plunge        variance        68% cone confidence cone 
#>      68.5127690      20.4958671       0.2168518      38.4502642       4.7492331

Plotting a summary of the stats on a equal-area projection:

stereoplot()
points(lines, col = "lightgrey", pch = 1, cex = .5)
points(lines_mean, col = "#B63679", pch = 19, cex = 1)
lines(lines_mean, ang = lines_confangle, col = "#E65164FF")
lines(lines_mean, ang = lines_delta, col = "#FB8861FF")
legend("topright", legend = c("Mean line", "95% confidence cone", "63% data cone"), col = c("#B63679", "#E65164FF", "#FB8861FF"), pch = c(19, NA, NA), lty = c(NA, 1, 1), cex = .75)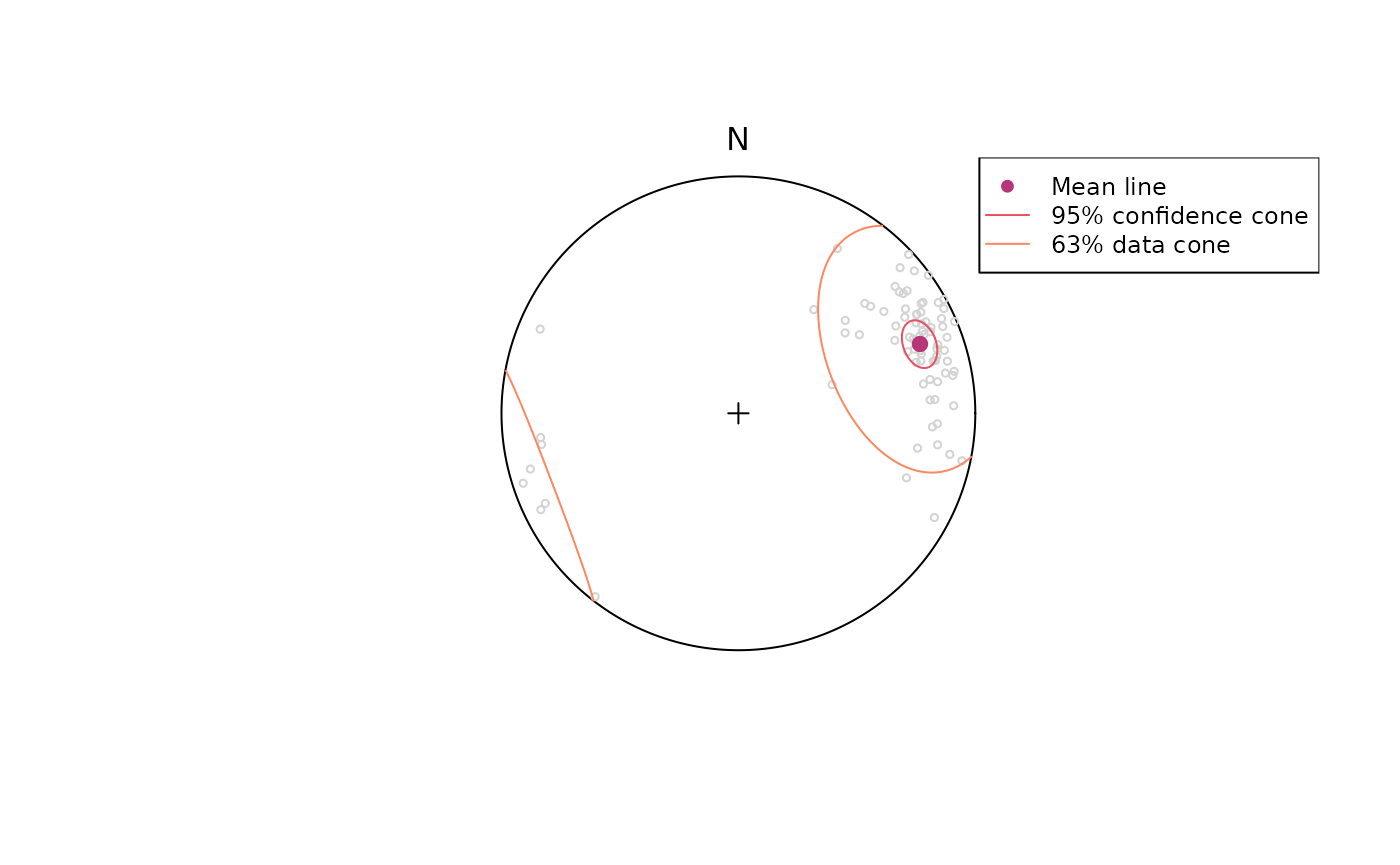

Diagram showing statistical results of some example data plotted in an equal-area projection

Geodesic mean and variance

Another measure of mean and dispersion is the Fréchet (geodesic L²) mean and variance which is based on the angles between all data vectors³.
This can be visualized using the variance_plot(); here showing the (geodesic) angle distances between all lines and the first line in the same data set:

variance_plot(lines, y = lines[1, ])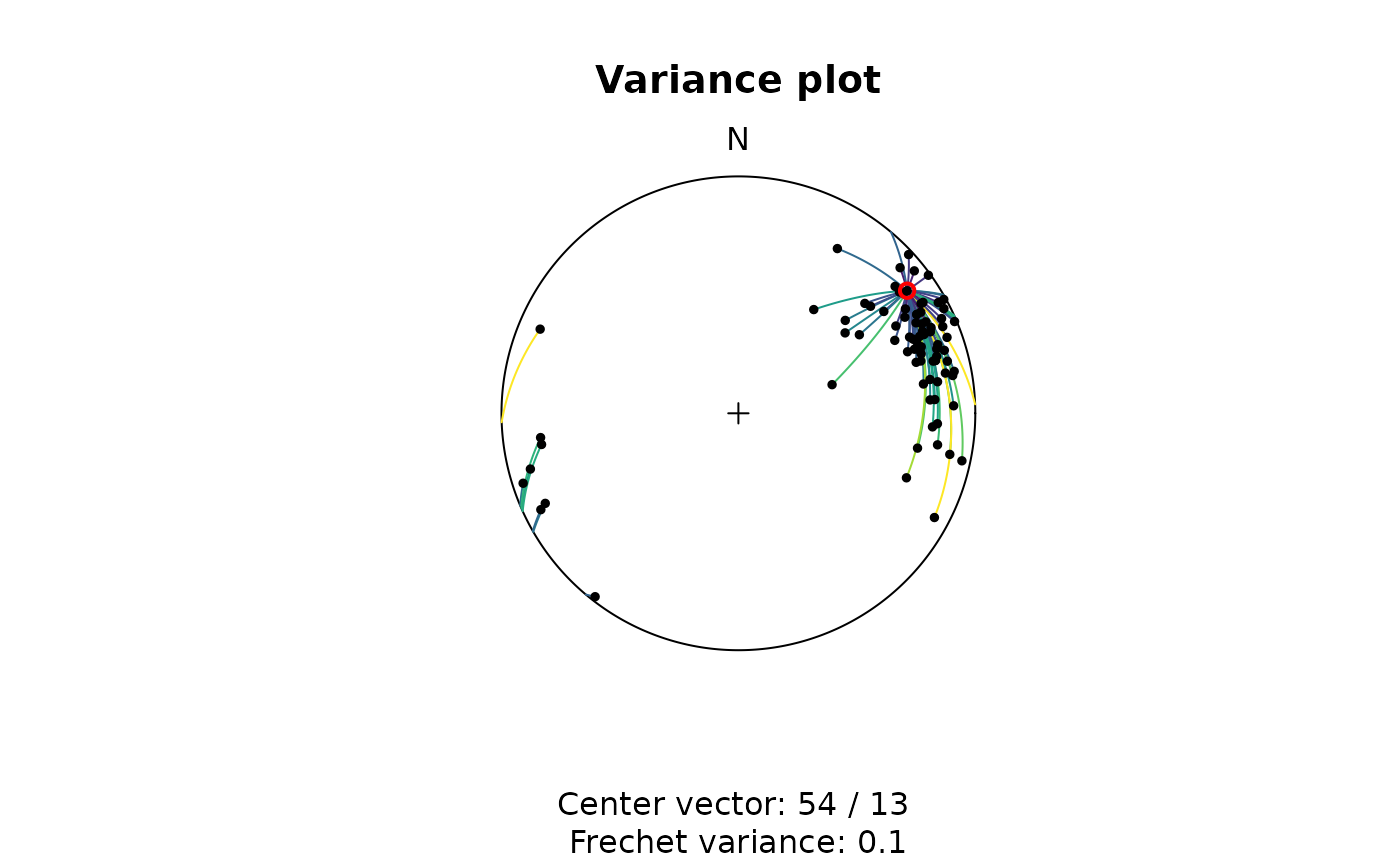

Diagram showing the distances of a set of vectors to a specified vector

The Fréchet mean is the vector that minimizes the sum of the squared angle distances to all data vectors. The Fréchet variance about this mean is the sum of the squared angle distances between all data vectors and the Fréchet mean.

To find the Fréchet mean vector, the algorithm iteratively searches for the vector by using a numerical optimization method to minimize the distances to all other vectors

# Mean
geodesic_mean(lines)
#> Line object (n = 1):
#>  azimuth   plunge 
#> 69.64061 14.87921

# Variance
geodesic_var(lines)
#> [1] 0.06118261

These estimators are good descriptors of the concentration of the data around the mean direction, when data follows a unimodal, anisotropic distributions such as the Kent or Bingham distributions.

Projected mean

The Eigenvector with the largest Eigenvalue represents a vector parallel to the highest concentration of a population. This vector can also be described as the projected mean. A shortcut function for this is:

projected_mean(example_lines)
#> Line object (n = 1):
#>  azimuth   plunge 
#> 69.09796 14.82125

These estimators are good descriptors of the concentration of the data around the mean direction, when data follows an unimodal, anisotropic distributions such as the Kent or Bingham distributions.

par(mfrow = c(1, 2))
stereoplot()
points(example_lines, col = "grey", pch = 16, cex = .7)
points(sph_mean(example_lines), col = "#1D1147FF", pch = 16)
points(geodesic_mean(example_lines), col = "#B63679FF", pch = 16)
points(projected_mean(example_lines), col = "#FEC287FF", pch = 16)
title(main = "Lines")

legend("bottomleft",
  legend = c("Arithmetic mean", "Geodesic mean", "Projected mean"),
  col = c("#1D1147FF", "#B63679FF", "#FEC287FF"),
  pch = 16,
  bg = "white"
)

stereoplot()
points(example_planes, col = "grey", pch = 16, cex = .7)
points(sph_mean(example_planes), col = "#1D1147FF", pch = 16)
points(geodesic_mean(example_planes), col = "#B63679FF", pch = 16)
points(projected_mean(example_planes), col = "#FEC287FF", pch = 16)
title(main = "Planes")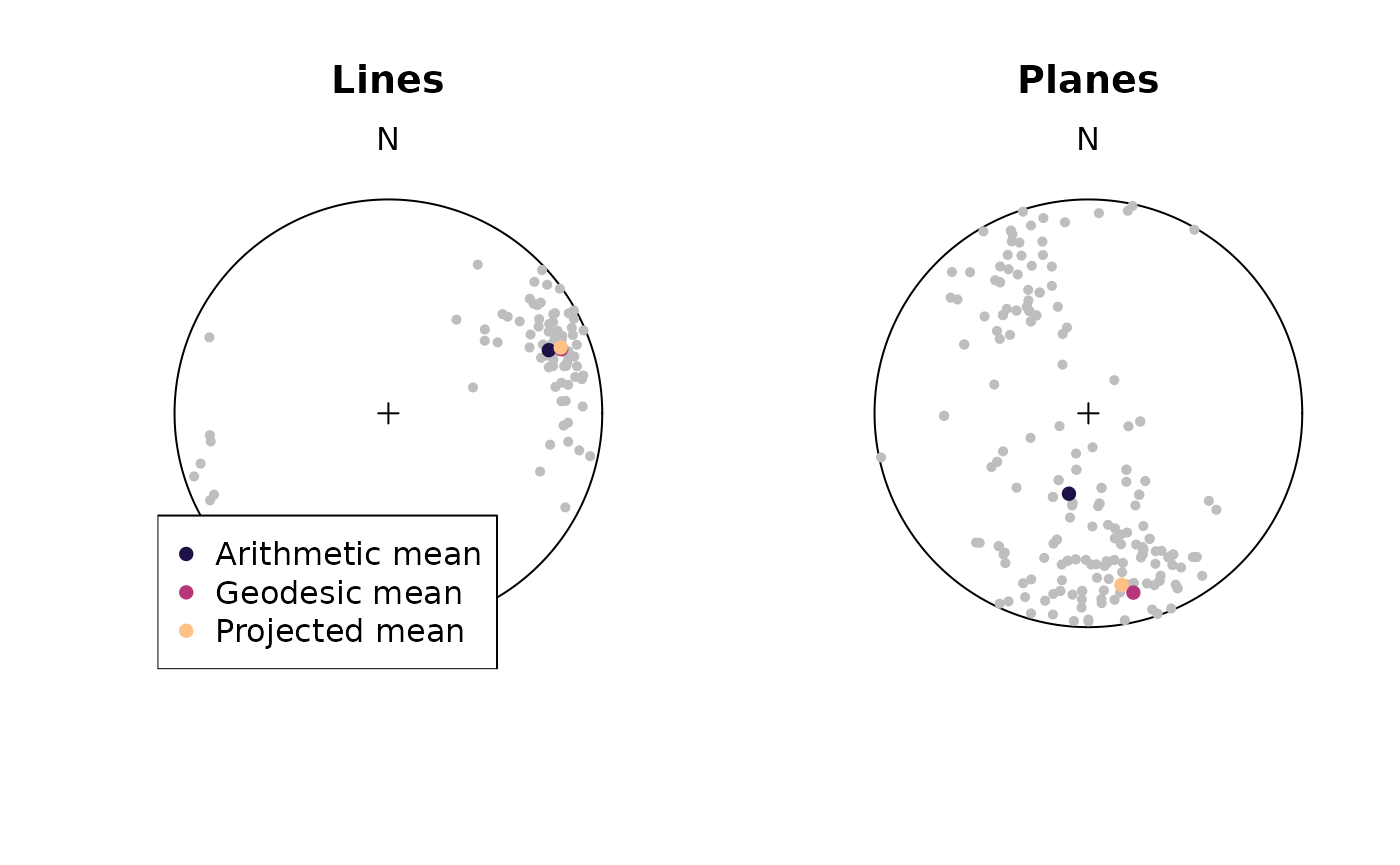

Equal area projections showing the different estimators of the mean

Hypothesis testing

Confidence region

To test if a line represents the population mean of a given set of lineations, we need to calculate the confidence region of our population.

Let’s test the hypothesis that a horizontal lineation trending towards 70° is the mean for our lineations.

line_NULL <- Line(70, 0)

The 95% confidence interval (from 10,000 bootstrap samples):

ce <- confidence_ellipse(lines, n = 10000, alpha = 0.05)

To visualize the confidence region of our lines:

plot(lines, col = "grey")
stereo_confidence(ce, col = "#B63679FF")
points(line_NULL, col = "#000004", pch = 16)

Diagram showing the confidence region of a mean

The $p$ -value for our hypothesis line:

ce$pvalue.FUN(line_NULL)
#> [1] 0

With (95% confidence) we rejected the Null Hypothesis that the given line represents the population mean as the p-value is smaller than 5%.

Two-sample T-Test

Wellner’s Rayleigh-style T-statistic⁴ measures how different two sets of vectors are. The test statistic T is a non-negative measure of dissimilarity between two datasets. The value is zero when the datasets are identical.

wellner(lines, line_NULL)
#> [1] 0.9585258

A $p$ -value for this test-statistic can be estimated using permutations. The fraction of tests in the computed T-statistic exceeds the observed T for the original data (a number between 0 and 1 inclusive) can be interpreted as a $p$ -value for the null hypothesis that the two populations are identical (not merely that their means coincide). Thus, smaller p-values indicate stronger evidence that the two populations differ significantly.

wellner_inference(lines, line_NULL, n_perm = 1000)
#> [1] 0.43

Orientation tensor

Eigenvectors

The orientation tensor⁵ is a matrix comprising the mean direction cosines of the orientation vectors. In case of a Bingham distribution, the Eigenvectors of this tensor describe the orientation of the most dense, intermediate and least dense orientation, and thus, are used to determine the orientation of girdle-distributed vectors (e.g. folded planes).

The orientation tensor of orientation tensor is calculated by ortensor():

ortensor(planes)
#> Orientation tensor
#>            [,1]        [,2]        [,3]
#> [1,]  0.5634412 -0.11043381 -0.12507927
#> [2,] -0.1104338  0.13269479 -0.04040902
#> [3,] -0.1250793 -0.04040902  0.30386403

The Eigenvalues from orientation data can be computed through ot_eigen()

planes_eigen <- ot_eigen(planes)
print(planes_eigen)
#> eigen() decomposition
#> $values
#> [1] 0.62975929 0.28812045 0.08212026
#> 
#> $vectors
#> Line object (n = 3):
#>        azimuth   plunge
#> [1,] 169.08091 19.46169
#> [2,] 300.98901 62.11934
#> [3,]  72.03016 19.15562

To visualize the orientation of the Eigenvectors and their -values, you can call the vectors and values of the object returned by ot_eigen():

stereoplot()
points(example_planes, col = "grey", pch = 16, cex = .7)
lines(planes_eigen$vectors, 
       col = c("#000004", "#B63679FF", "#FEC287FF"), 
       lwd = rev(assign_cex(planes_eigen$values, range = c(.5, 2))))
points(planes_eigen$vectors, 
       col = c("#000004", "#B63679FF", "#FEC287FF"), 
       cex = assign_cex(planes_eigen$values, range = c(.5, 2)), 
       pch = 16)
legend('right', 
       legend = c("Eigen-1", "Eigen-2", "Eigen-3"), 
       col = c("#000004", "#B63679FF", "#FEC287FF"), pch = 16, lty = 1)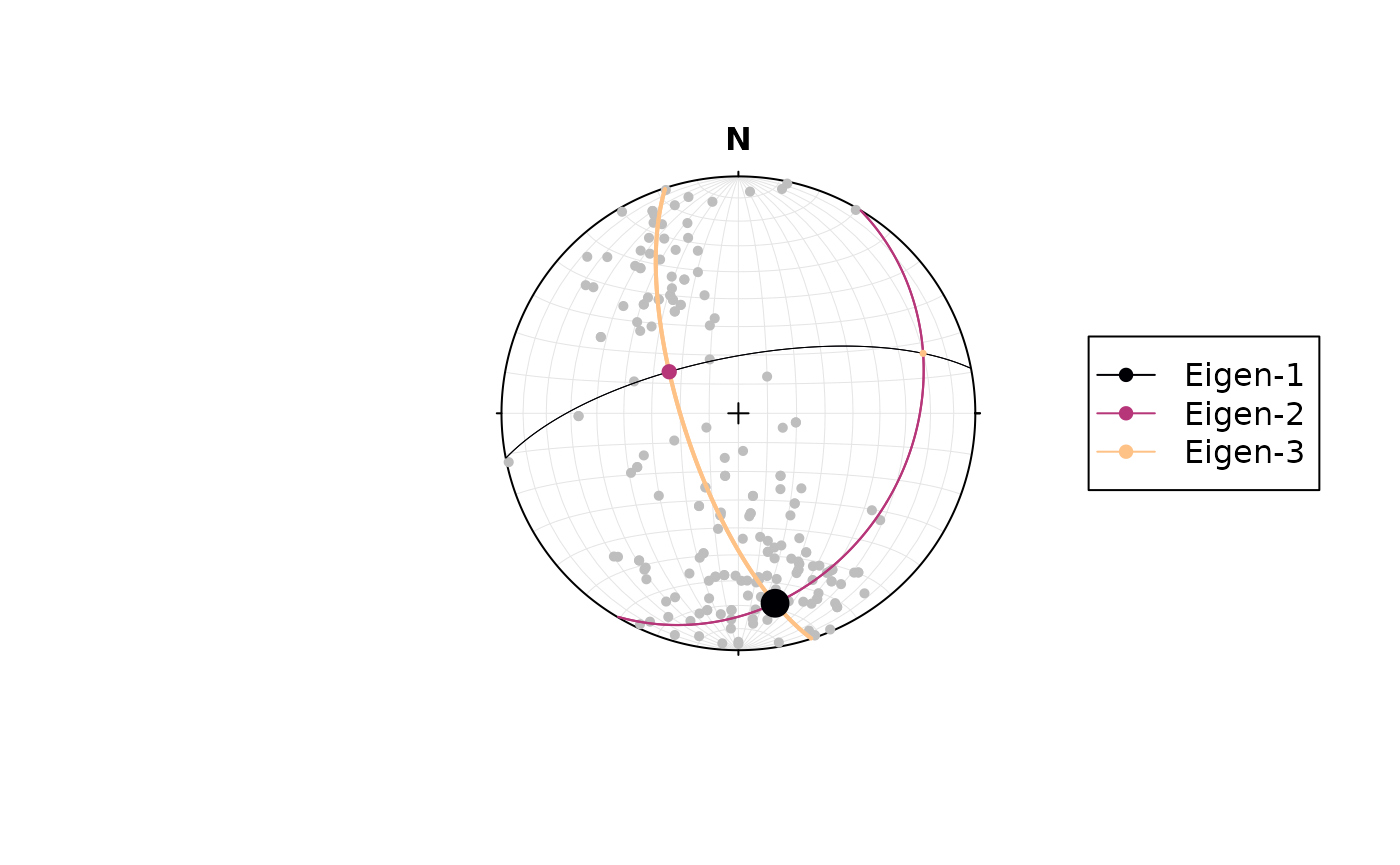

Shape parameters

There are more shape parameters using different algorithms based on the orientation tensor:

shape_params(planes)
#> $stretch_ratios
#>      Rxy      Ryz      Rxz 
#> 1.478428 1.873104 2.769250 
#> 
#> $strain_ratios
#>       e12       e13       e23 
#> 0.3909795 1.0185765 0.6275970 
#> 
#> $Flinn
#> $Flinn$k
#> [1] 0.5479625
#> 
#> $Flinn$d
#> [1] 0.9955924
#> 
#> 
#> $Ramsay
#> intensity  symmetry 
#> 0.5467429 0.6229787 
#> 
#> $Woodcock
#>  strength     shape 
#> 1.0185765 0.6229787 
#> 
#> $Watterson_intensity
#> [1] 2.351532
#> 
#> $Lisle_intensity
#> [1] 1.147654
#> 
#> $Nadai
#>      goct      eoct 
#> 0.8391109 0.7266914 
#> 
#> $Lode
#> [1] 0.2323021
#> 
#> $kind
#> [1] "SSL"
#> 
#> $MAD
#> [1] 32.80303
#> 
#> $Jellinek
#> [1] 2.794622

Cluster vectors

To find k clusters of orientational data, the sph_cluster() function can be used:

# generate some random vectors:
x1 <- rvmf(100, mu = Line(90, 0), k = 20)
x2 <- rvmf(100, mu = Line(0, 0), k = 20)
x3 <- rvmf(100, mu = Line(0, 90), k = 20)
x123 <- rbind(x1, x2, x3)

# cluster the vectors:
cl <- sph_cluster(x123, k = 3)

# visualize the result:
plot(x123, col = assign_col_d(cl$cluster))

legend_col_d(assign_col_d(unique(cl$cluster)), title = "Cluster")

Stereoplot showing the the cluster result of an example dataset

References

Bachmann, F., Hielscher, R., Jupp, P. E., Pantleon, W., Schaeben, H., & Wegert, E. (2010). Inferential statistics of electron backscatter diffraction data from within individual crystalline grains. Journal of Applied Crystallography, 43(6), 1338–1355. https://doi.org/10.1107/S002188981003027X

Davis, J. R., & Titus, S. J. (2017). Modern methods of analysis for three-dimensional orientational data. Journal of Structural Geology, 96, 65–89. https://doi.org/10.1016/j.jsg.2017.01.002

Mardia, K. V., & Jupp, P. E. (2000). Directional Statistics. (K. V. Mardia & P. E. Jupp, Eds.). Hoboken, NJ, USA: Wiley. https://doi.org/10.1002/9780470316979

Scheidegger, A. E. (1964). The tectonic stress and tectonic motion direction in Europe and Western Asia as calculated from earthquake fault plane solutions. Bulletin of the Seismological Society of America, 54(5A), 1519–1528. https://doi.org/10.1785/BSSA05405A1519

Wellner, J. A. (1979) “Permutation Tests for Directional Data.” Ann. Statist. 7(5) 929-943. https://doi.org/10.1214/aos/1176344779

Tobias Stephan

2025-11-22