Strain and Vorticity Analysis

Tobias Stephan

2025-11-02

This tutorial demonstrates how to perform strain and vorticity analysis using the {structr} package in R.

library(structr)

Strain analysis

Import some Rf/ϕ data from elliptical strain markers

data(ramsay)
head(ramsay)
#>         R   phi
#> [1,] 1.24 35.96
#> [2,] 1.52 27.59
#> [3,] 1.33 36.91
#> [4,] 1.78 27.31
#> [5,] 1.51 17.73
#> [6,] 1.70 24.45

The mean mean strain ellipse (shape and orientation) of deformed elliptical objects as strain markers can be calculated by using the mean shape matrix and its eigenvalues¹:

ramsay_mean <- mean_strain_ellipse(r = ramsay[, 1], phi = ramsay[, 2])
print(ramsay_mean)
#> $R
#> [1] 1.628138
#> 
#> $phi
#> [1] 25.73632
#> 
#> $R_CI
#> [1] 1.59275 1.66359
#> 
#> $phi_CI
#> [1] 24.71905 26.75180

The {structr} algorithm also calculates bootstrapped 95% confidence interval.

To visualize the distribution of the strain values, we can calculate densities in Rf/ϕ space² and plot them in a Rf/ϕ diagram³:

Rphi_plot(r = ramsay[, 1], phi = ramsay[, 2])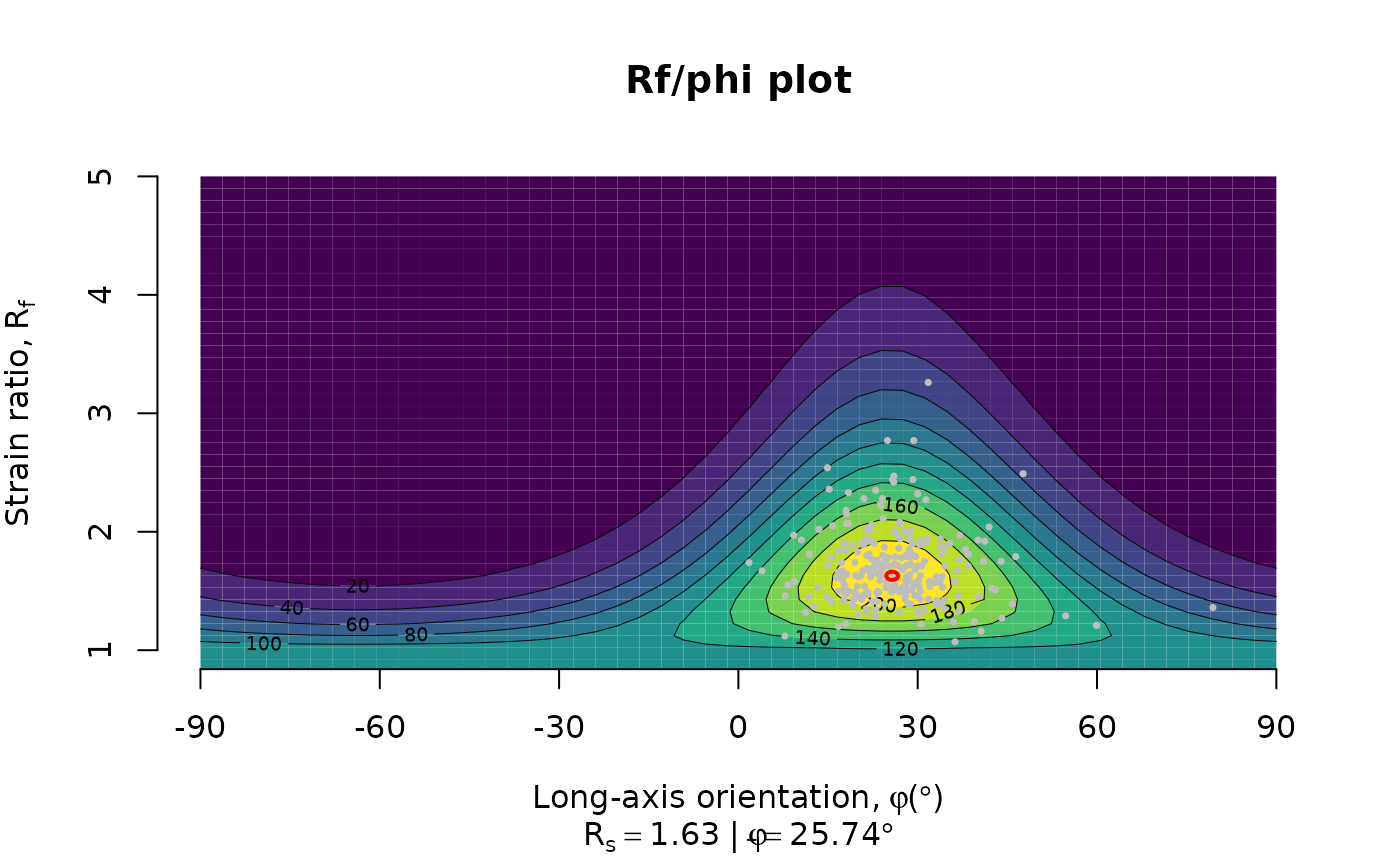

or in an Equidistant polar plot⁴:

Rphi_polar_plot(ramsay[, 1], ramsay[, 2], proj = "eqd")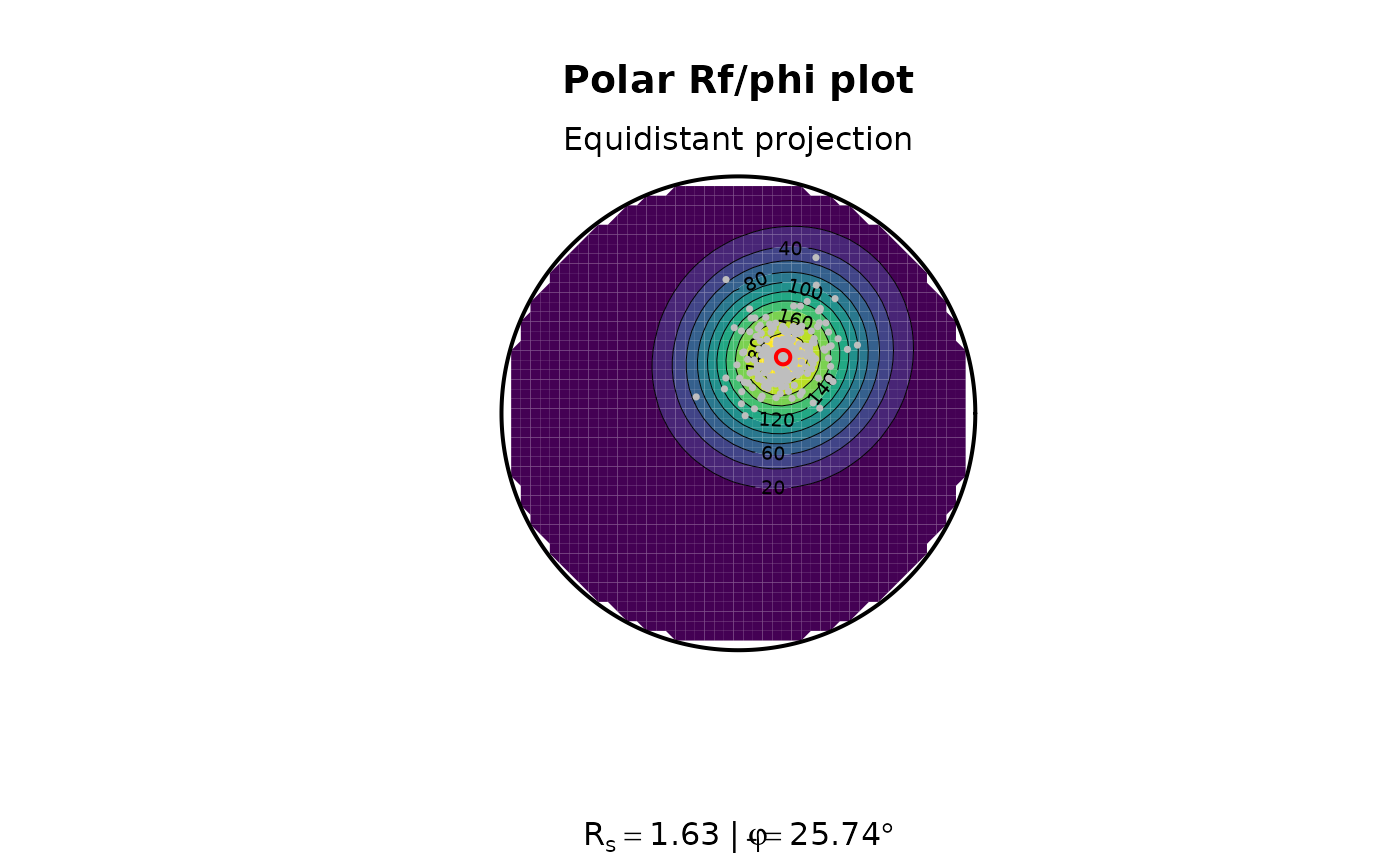

3D Strain

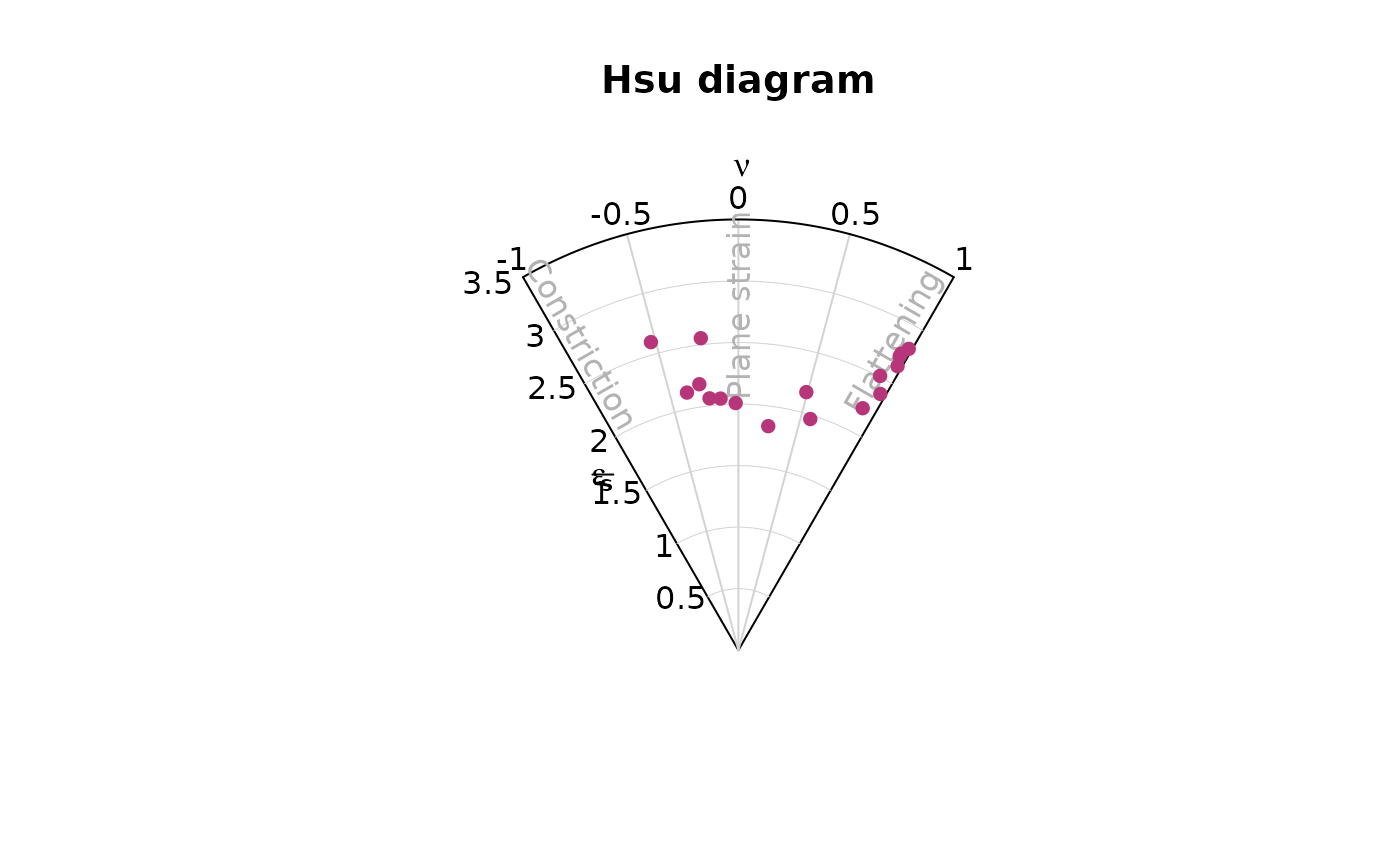
Three-dimensional strain data are expressed by the ratio of the magnitudes of the 3 principal strain axes of the strain ellipsoid, $X \geq Y \geq Z$. They can be represented in the Flinn diagram⁵, either linear or logarithmic.

data("holst")
R_XY <- holst[, "R_XY"]
R_YZ <- holst[, "R_YZ"]

flinn_plot(R_XY, R_YZ, log = TRUE, col = "#B63679", pch = 16)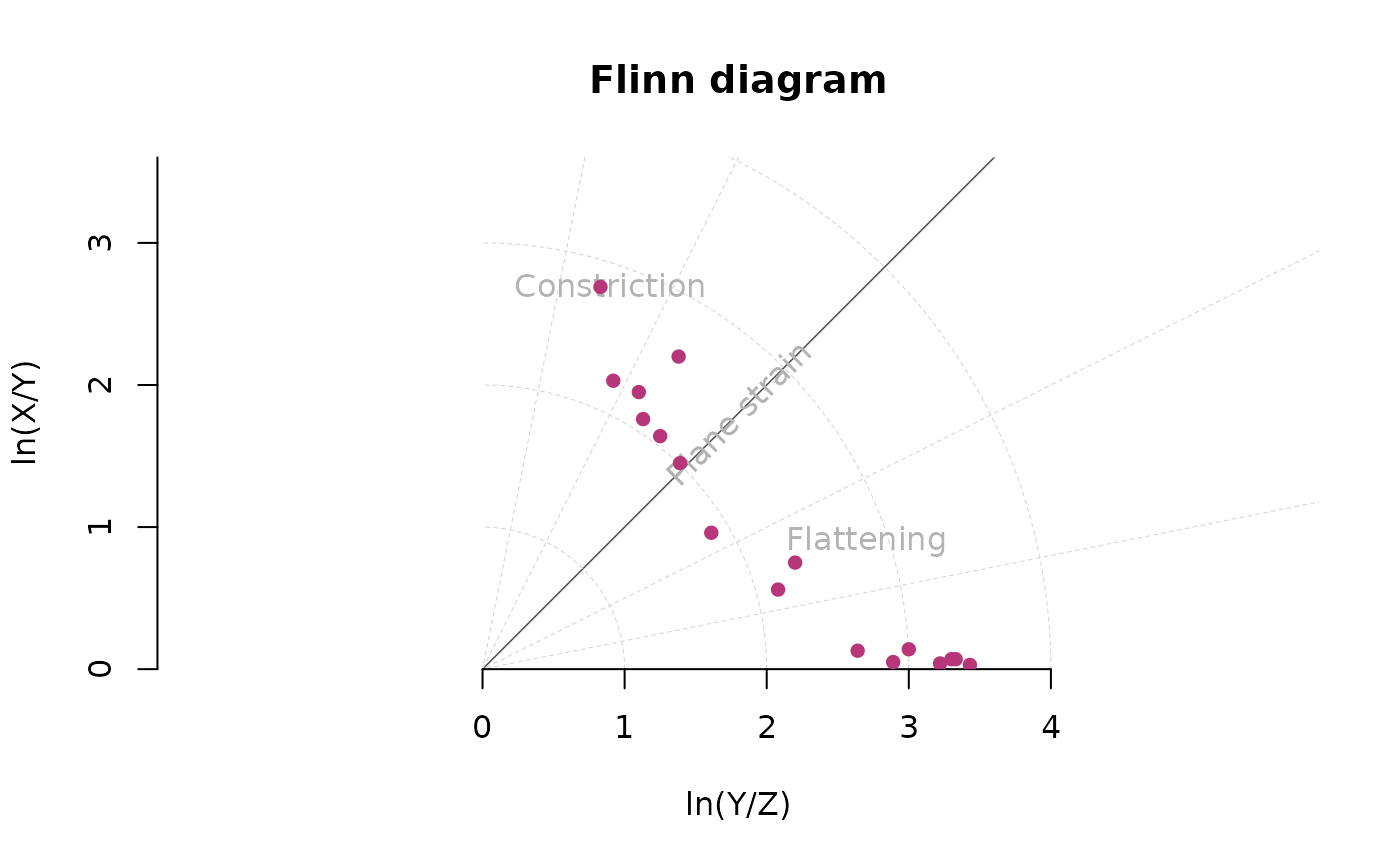

or the Hsu diagram⁶ using the natural octahedral unit strain⁷ ($\bar{\epsilon}_s$) and the Lode parameter⁸ ($\nu$):

hsu_plot(R_XY, R_YZ, col = "#B63679", pch = 16)

Vorticity analysis

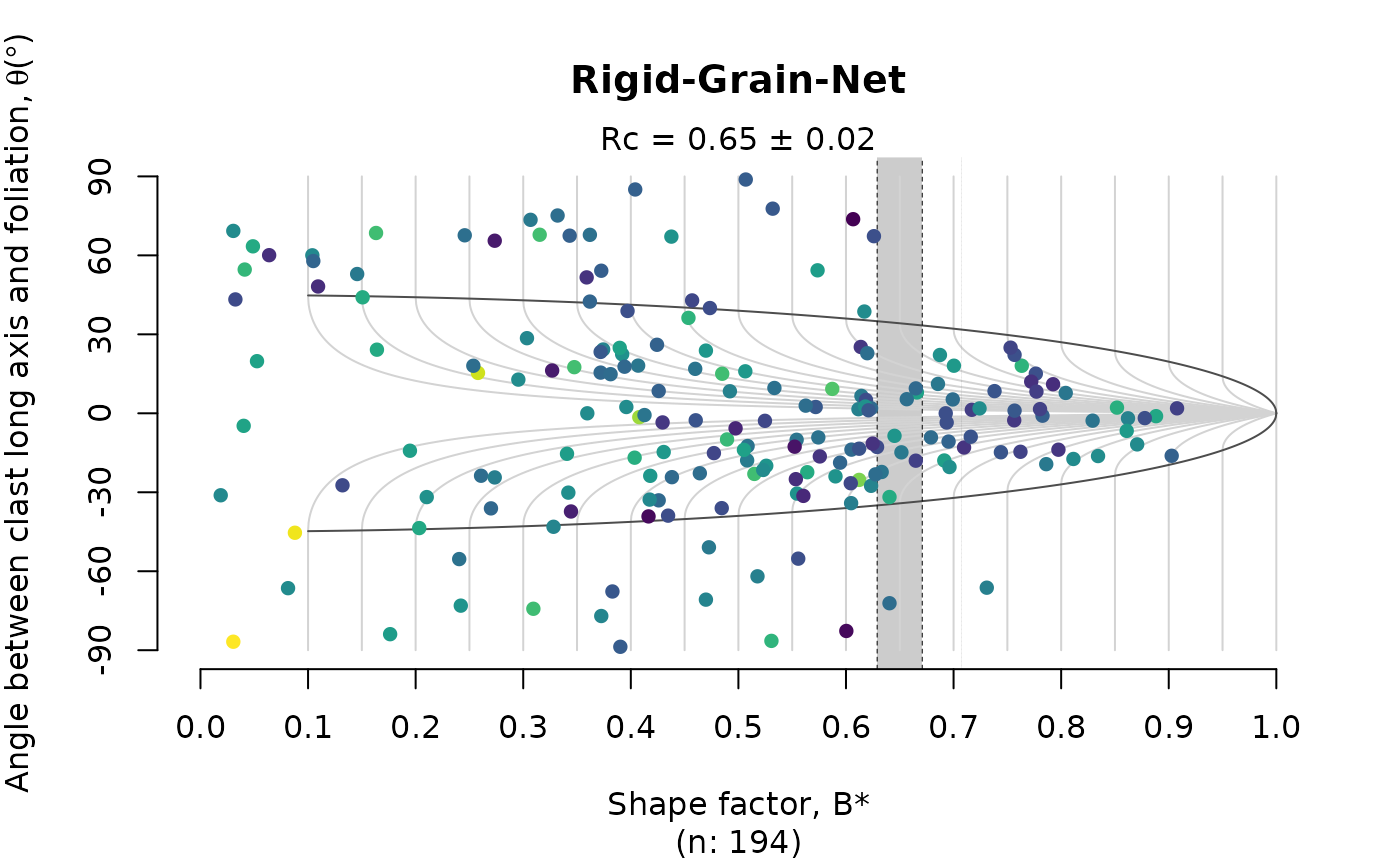
The rigid grain net after (Jessup et al. 2007)⁹ plots the distribution the strain ratio (R) of orientation (phi) of porphyroclast over the theoretical distribution of tailless clasts. The plot estimates the critical threshold Rc marking the transition between the stable-sink position and infinitely rotating porphyroclasts. This threshold can be interpreted as the the mean kinematic vorticity number. Here the Rc is estimated using the bootstrap method described in Stephan et al. (2025)¹⁰.

data(shebandowan)
set.seed(20250411)

# Color code porphyroclasts by size of clast (area in log-scale):
RGN_plot(shebandowan$r, shebandowan$phi, col = assign_col(log(shebandowan$area)), pch = 16)