2. Stereographic projections

library(structr)

Import and convert to spherical objects:

data(example_planes)
data(example_lines)

planes <- Plane(example_planes$dipdir, example_planes$dip)
lines <- Line(example_lines$trend, example_lines$plunge)

Stereographic projection

Lambert equal area, lower hemisphere projection is the default plotting setting.

stereoplot()
points(lines, col = "#B63679", pch = 19, cex = .5)
points(planes, col = "#000004", pch = 1, cex = .5)
legend("topright", legend = c("Lines", "Planes"), col = c("#B63679", "#000004"), pch = c(19, 1), cex = 1)
title(main = "Example data", sub = "Lambert equal area, lower hemisphere projection")

Diagram showing the equal-area Lambert projection of some example data

To change to equal angle stereographic, upper hemisphere projection

stereoplot(earea = FALSE)
points(lines, col = "#B63679", pch = 19, cex = .5, earea = FALSE, upper.hem = TRUE)
points(planes, col = "#000004", pch = 1, cex = .5, earea = FALSE, upper.hem = TRUE)
legend("topright", legend = c("Lines", "Planes"), col = c("#B63679", "#000004"), pch = c(19, 1), cex = 1)
title(main = "Example data", sub = "Equal angle stereographic, upper hemisphere projection")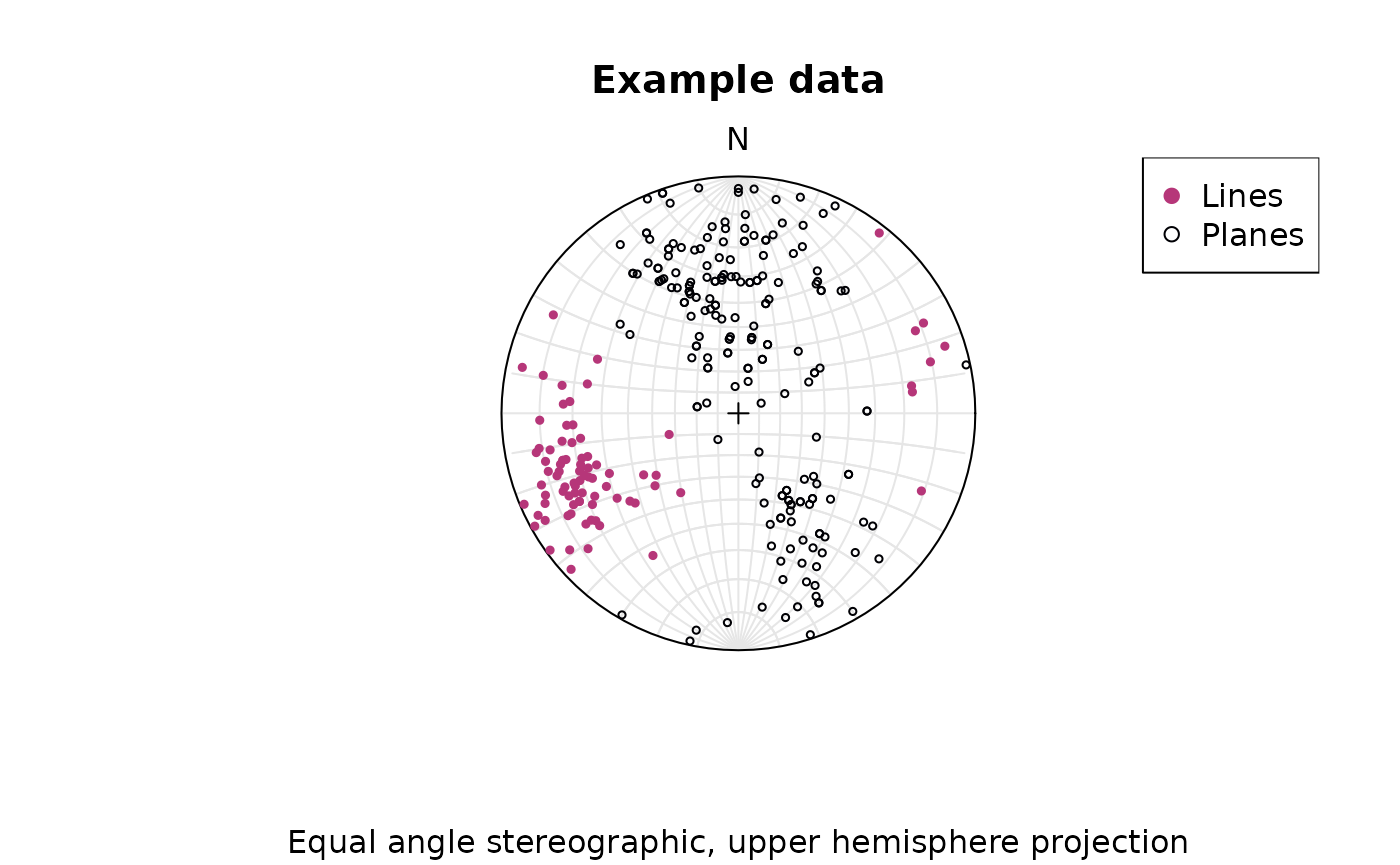

Diagram showing the equal-angle stereographic projection of some example data

Adding great circles:

stereoplot(guides = FALSE)
lines(planes, col = "lightgrey", lty = 1)
points(planes, col = "#000004", pch = 1, cex = .5)

Diagram showing greatcircles

Statistics

example_lines$quality <- ifelse(is.na(example_lines$quality), 6, example_lines$quality) # replacing NA values with 6
line_weightings <- 6 / example_lines$quality

The (weighted) mean orientation

lines_mean <- sph_mean(lines, w = line_weightings)

The (weighted) variance

lines_variance <- sph_var(lines, w = line_weightings)

the (weighted) standard deviation (i.e. the 63% cone around the mean) and the 95% confidence cone around the mean:

lines_delta <- delta(lines, w = line_weightings)
lines_confangle <- sph_confidence_angle(lines, w = line_weightings)

Taken together, this prints as

c(
  "Variance" = lines_variance,
  "63% cone" = lines_delta,
  "Confidence angle" = lines_confangle
)
#>         Variance         63% cone Confidence angle 
#>        0.1938084       36.2745102        6.9017035

Summary stats can also be retrieved through

summary(lines)
#>         azimuth          plunge        variance        68% cone confidence cone 
#>      68.5127690      20.4958671       0.2168518      38.4502642       4.7492331

Plotting a summary of the stats on a equal-area projection:

stereoplot(guides = FALSE)
points(lines, col = "lightgrey", pch = 1, cex = .5)
points(lines_mean, col = "#B63679", pch = 19, cex = 1)
lines(lines_mean, ang = lines_confangle, col = "#E65164FF")
lines(lines_mean, ang = lines_delta, col = "#FB8861FF")
legend("topright", legend = c("Mean line", "95% confidence cone", "63% data cone"), col = c("#B63679", "#E65164FF", "#FB8861FF"), pch = c(19, NA, NA), lty = c(NA, 1, 1), cex = .75)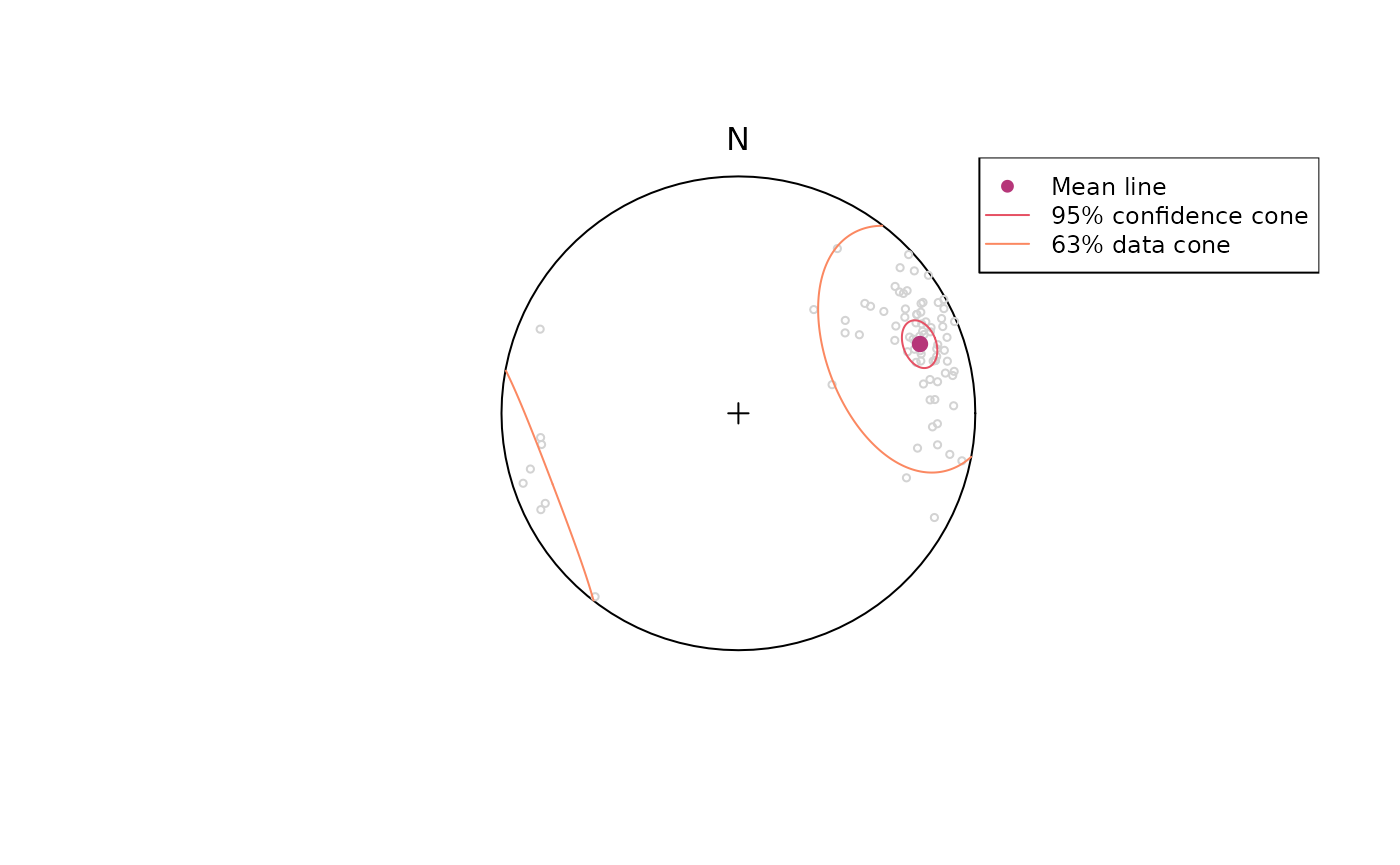

Diagram showing statistical results of some example data plotted in an equal-area projection

Orientation tensor

Eigenvectors

The orientation tensor (Scheidegger 1965) is a matrix comprised of all direction cosines of the orientation vectors. In case of a Bingham distribution, the eigenvectors of this tensor describe the orientation of the most dense, intermediate and least dense orientation, and thus, are used to determine the orientation of girdle-distributed vectors (e.g. folded planes).

planes_eigen <- ot_eigen(planes)

stereoplot(guides = FALSE)
points(planes, col = "lightgrey", pch = 1, cex = .5)
lines(planes_eigen$vectors, col = viridis::magma(3), lty = 1)
points(planes_eigen$vectors, col = viridis::magma(3), pch = 19, cex = 1)
legend("topright", legend = c("Eigenvectors 1", "Eigenvectors 2", "Eigenvectors 3"), col = viridis::magma(3), pch = 19, cex = .75)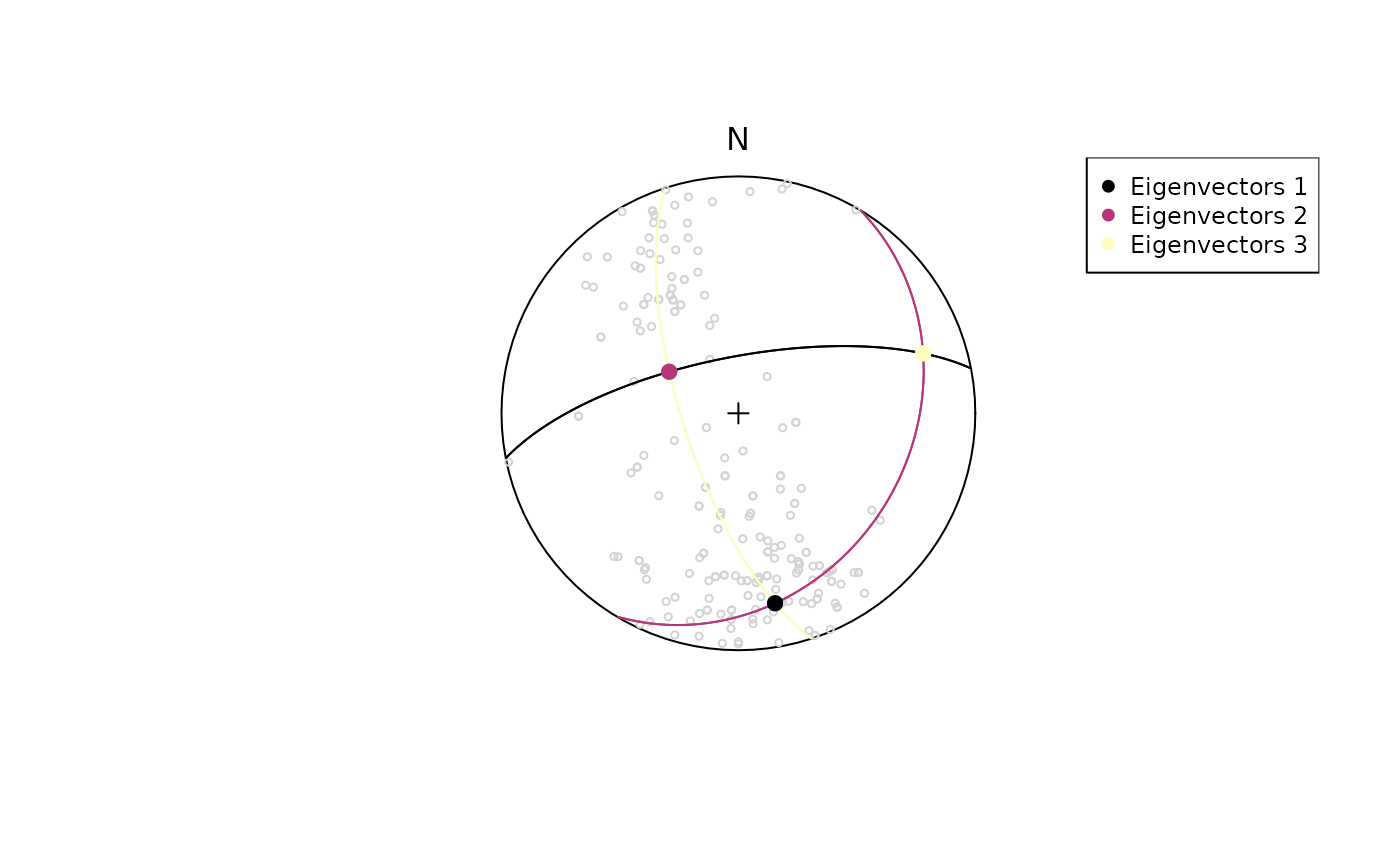

Diagram showing eigen-vector analysis of some example data plotted in an equal-area projection

Eigenvalues

The eigenvalues of the orientation tensor. describe the shape of the distribution of these vectors, that is who clustered, cylindrical or random these vectors are distributed.

A Fabric plot visualizes the shape of the distribution by plotting the eigenvalues of the orientation tensor. Two different diagram are provided by {structr}, namely the triangular Vollmer plot after Vollmer (1990) and the logarithmic biplot (Woodcock plot) after Woodcock (1977).

Vollmer plot

vollmer_plot(planes, col = "#000004", pch = 1, cex = 2)
vollmer_plot(lines, add = TRUE, col = "#B63679", pch = 19, cex = 2)
legend("topright", legend = c("Lines", "Planes"), col = c("#B63679", "#000004"), pch = c(19, 1), cex = 1)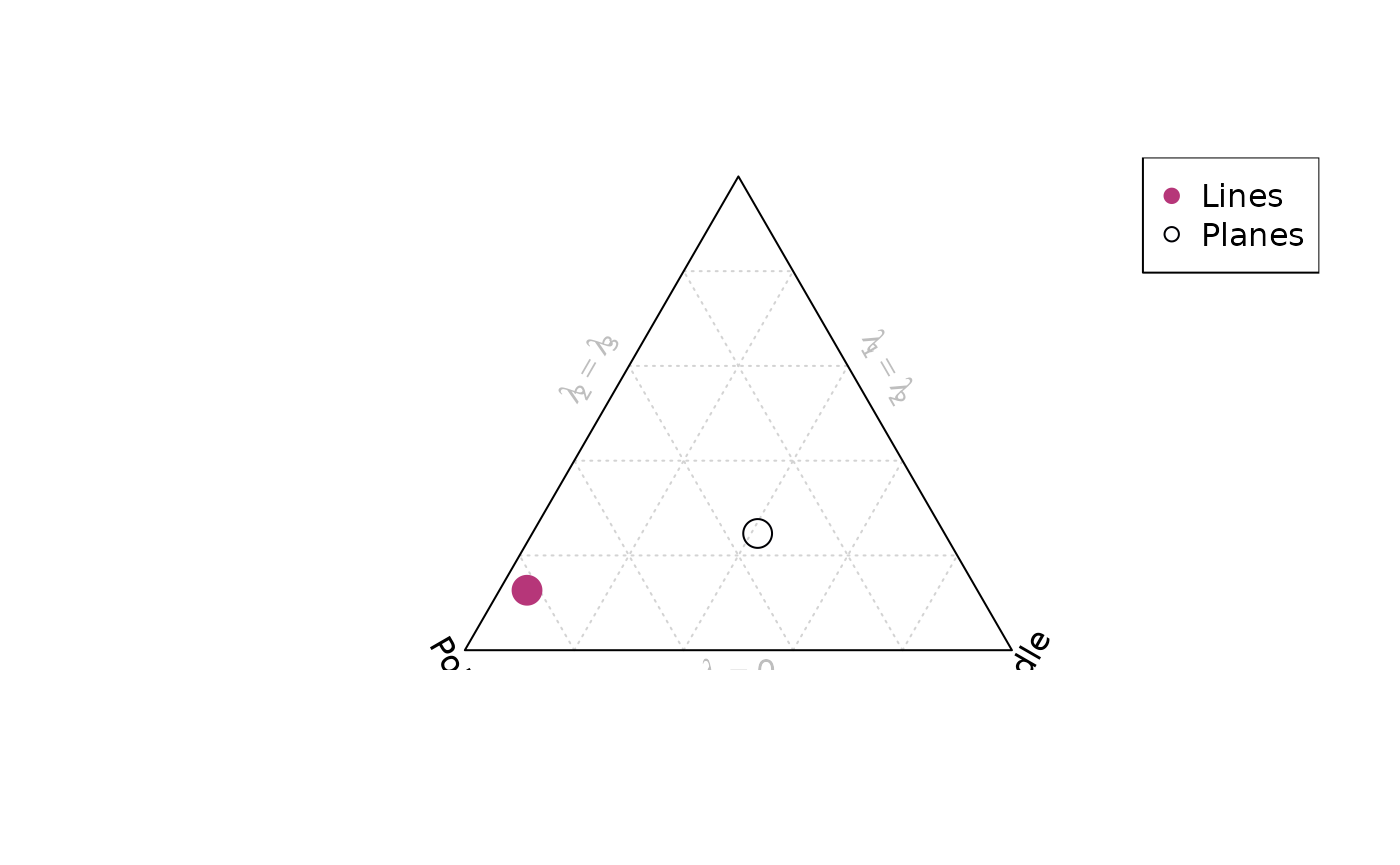

Diagram showing eigen-vector analysis of some example data plotted in an triangular plot after Vollmer 1990

Woodcock plot

woodcock_plot(planes, col = "#000004", pch = 1, cex = 2)
woodcock_plot(lines, add = TRUE, col = "#B63679", pch = 19, cex = 2)
legend("topright", legend = c("Lines", "Planes"), col = c("#B63679", "#000004"), pch = c(19, 1), cex = 1)

Diagram showing eigen-vector analysis of some example data plotted in an biplot plot after Woodcok 1977

Hsü plot

hsu_fabric_plot(planes, col = "#000004", pch = 1, cex = 2)
hsu_fabric_plot(lines, add = TRUE, col = "#B63679", pch = 19, cex = 2)
legend("topright", legend = c("Lines", "Planes"), col = c("#B63679", "#000004"), pch = c(19, 1), cex = 1)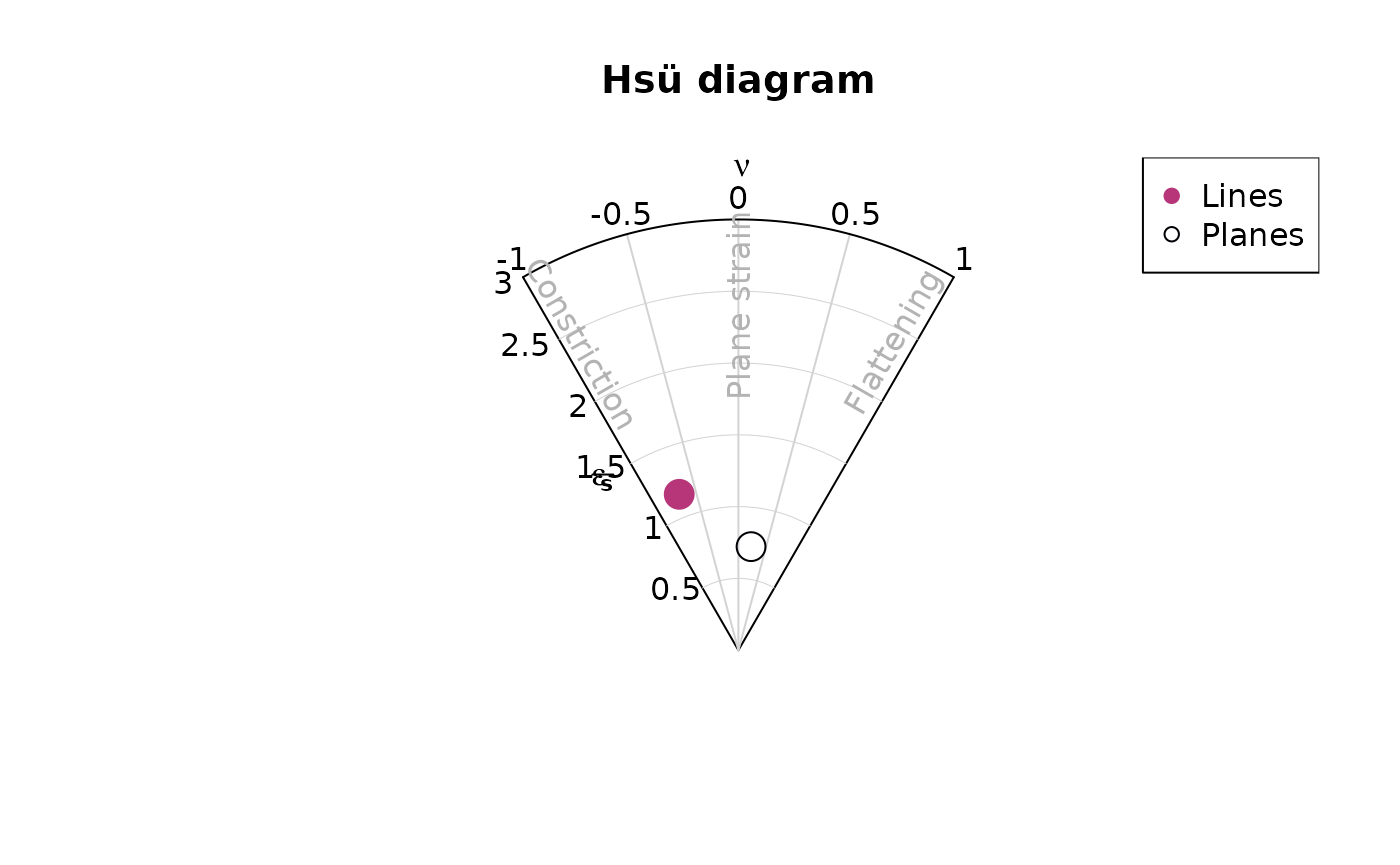

Diagram showing eigen-vector analysis of some example data plotted in a Hsü plot

Shape parameters

There are more shape parameters using different algorithms based on the orientation tensor:

or_shape_params(planes)
#> $stretch_ratios
#>      Rxy      Ryz      Rxz 
#> 1.478428 1.873104 2.769250 
#> 
#> $strain_ratios
#>       e12       e13       e23 
#> 0.3909795 1.0185765 0.6275970 
#> 
#> $Vollmer
#>          P          G          R          B          C          I          D 
#>  68.327769  82.400078  49.272153 150.727847   2.037153   1.147654 170.240224 
#> 
#> $Flinn
#> $Flinn$k
#> [1] 0.5479625
#> 
#> $Flinn$d
#> [1] 0.9955924
#> 
#> 
#> $Ramsay
#> intensity  symmetry 
#> 0.5467429 0.6229787 
#> 
#> $Woodcock
#>  strength     shape 
#> 1.0185765 0.6229787 
#> 
#> $Watterson_intensity
#> [1] 2.351532
#> 
#> $Lisle_intensity
#> [1] 144908.7
#> 
#> $Nadai
#>      goct      eoct 
#> 0.8391109 0.7266914 
#> 
#> $Lode
#> [1] 0.2323021
#> 
#> $kind
#> [1] "SSL"
#> 
#> $MAD
#> [1] 32.80303
#> 
#> $US
#> [1] 28981734
#> 
#> $Jellinek
#> [1] 2.794622

Density plots

Densities are estimated using Kamb contouring (after Kamb, 1959) and exponential (the default), linear, square-inverse or no smoothing. Weighted densities can be controlled by the weights argument and are useful when the orientation measurements have different accuracies.

example_planes$quality <- ifelse(is.na(example_planes$quality), 6, example_planes$quality) # replacing NA values with 6
plane_weightings <- 6 / example_planes$quality

fabric_p <- or_shape_params(planes)$Vollmer["D"]
fabric_l <- or_shape_params(lines)$Vollmer["D"]

par(mfrow = c(1, 2))
stereoplot(guides = TRUE, col = "grey96")
points(planes, col = "grey", pch = 16, cex = .5)
contour(planes, add = TRUE, weights = plane_weightings)
points(planes_eigen$vectors[3, ], col = "black", pch = 16)
lines(planes_eigen$vectors[3, ], col = "black", pch = 16)
title(
  main = "Planes",
  sub = paste0(
    "N: ", nrow(planes), " | Fabric strength: ", round(fabric_p, 2),
    "\nLambert equal area, lower hemisphere projection"
  )
)

stereoplot(guides = TRUE, col = "grey96")
points(lines, col = "grey", pch = 16, cex = .5)
contour(lines, add = TRUE, weights = line_weightings)
points(lines_mean, col = "black", pch = 16)
title(
  main = "Lines",
  sub = paste0(
    "N: ", nrow(lines), " | Fabric strength: ", round(fabric_l, 2),
    "\nLambert equal area, lower hemisphere projection"
  )
)

Diagram showing the density distribution some example data plotted in an equal-area projection

Fault plots

Fault objects consist of planes (fault plane), lines (e.g. striae), and the sense of movement. There are two ways how these combined features can be visualized, namely the Angelier and the Hoeppner plot.

Angelier plot

The Angelier plot shows all planes as great circles and lineations as points (after Angelier , 1984). Fault striae are plotted as vectors on top of the lineation pointing in the movement direction of the hangingwall. Easy to read in case of homogeneous or small datasets.

f <- Fault(
  c("a" = 120, "b" = 125, "c" = 100),
  c(60, 62, 50),
  c(110, 25, 30),
  c(58, 9, 23),
  c(1, -1, 1)
)

stereoplot(title = "Angelier plot")
angelier(f, col = viridis::magma(nrow(f), end = .9))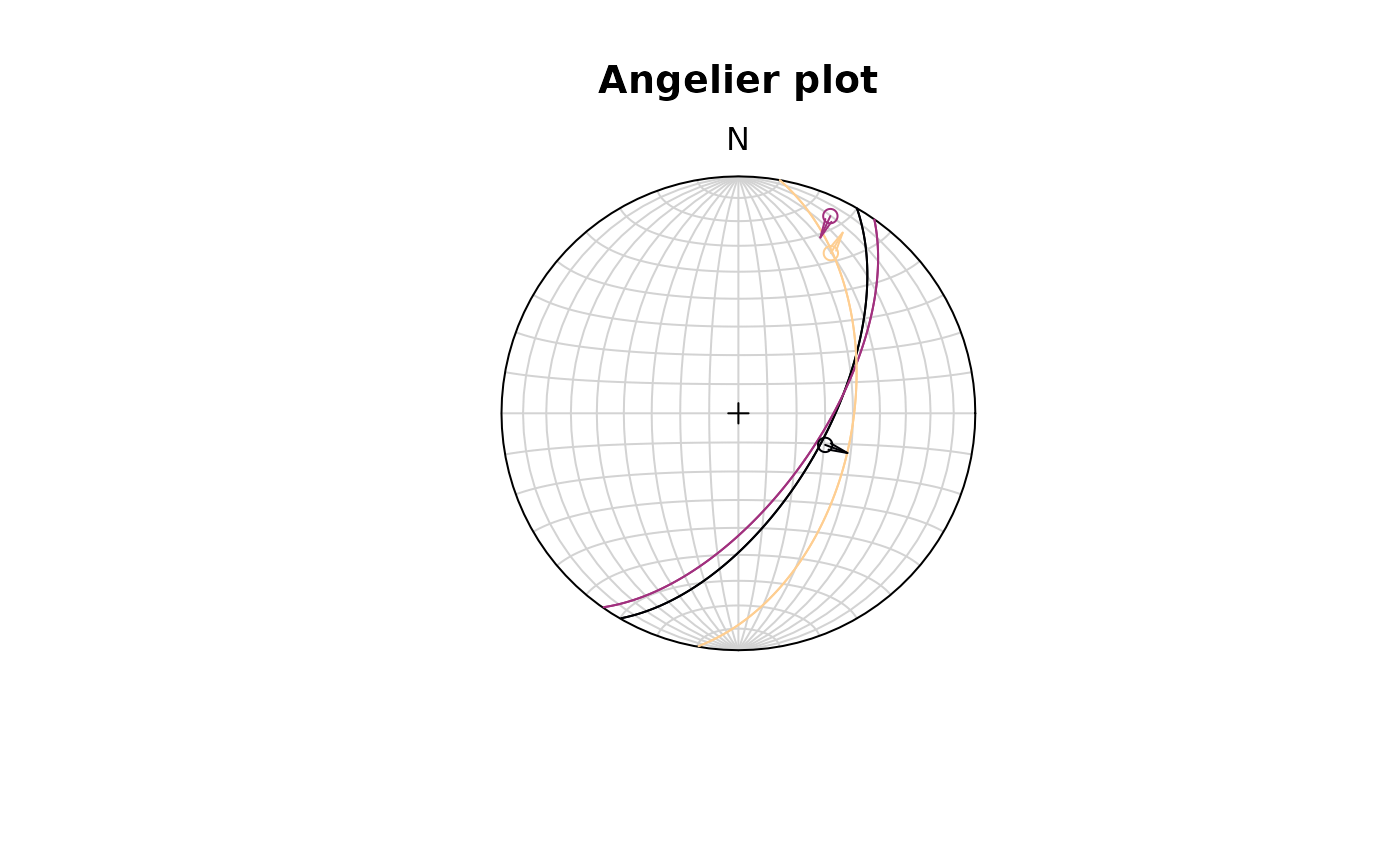

Diagram showing example fault data plotted in an equal-area projection

Hoeppner plot

The Hoeppner plot shows all planes as poles while lineations are not shown (after Hoeppner, 1955). Fault striae are plotted as vectors on top of poles pointing in the movement direction of the hangingwall. Useful in case of large or heterogeneous datasets.

stereoplot(title = "Hoeppner plot")
hoeppner(f, col = viridis::magma(nrow(f), end = .9))