4. Orientation Plots

This tutorial shows how to create various orientation plots using the {structr} package, including stereographic and equal-area projections, fabric plots, density plots, and fault plots.

library(structr)

Import and convert to spherical objects:

data(example_planes_df)
data(example_lines_df)

planes <- Plane(example_planes_df$dipdir, example_planes_df$dip)
lines <- Line(example_lines_df$trend, example_lines_df$plunge)

Equal-area projection

Lambert equal area, lower hemisphere projection is the default plotting setting.

stereoplot()
points(lines, col = "#B63679", pch = 19, cex = .5)
points(planes, col = "#000004", pch = 1, cex = .5)

legend("topright", legend = c("Lines", "Planes"), col = c("#B63679", "#000004"), pch = c(19, 1), cex = 1)
title(main = "Example data", sub = "Lambert equal area, lower hemisphere projection")

Diagram showing the equal-area Lambert projection of some example data

Points can be added using the points() function.

Stereographic projection

To change to equal angle stereographic, upper hemisphere projection, just set the earea argument to FALSE, and the upper.hem argument to TRUE:

stereoplot(earea = FALSE)
points(lines, col = "#B63679", pch = 19, cex = .5, earea = FALSE, upper.hem = TRUE)
points(planes, col = "#000004", pch = 1, cex = .5, earea = FALSE, upper.hem = TRUE)

legend("topright", legend = c("Lines", "Planes"), col = c("#B63679", "#000004"), pch = c(19, 1), cex = 1)
title(main = "Example data", sub = "Equal angle stereographic, upper hemisphere projection")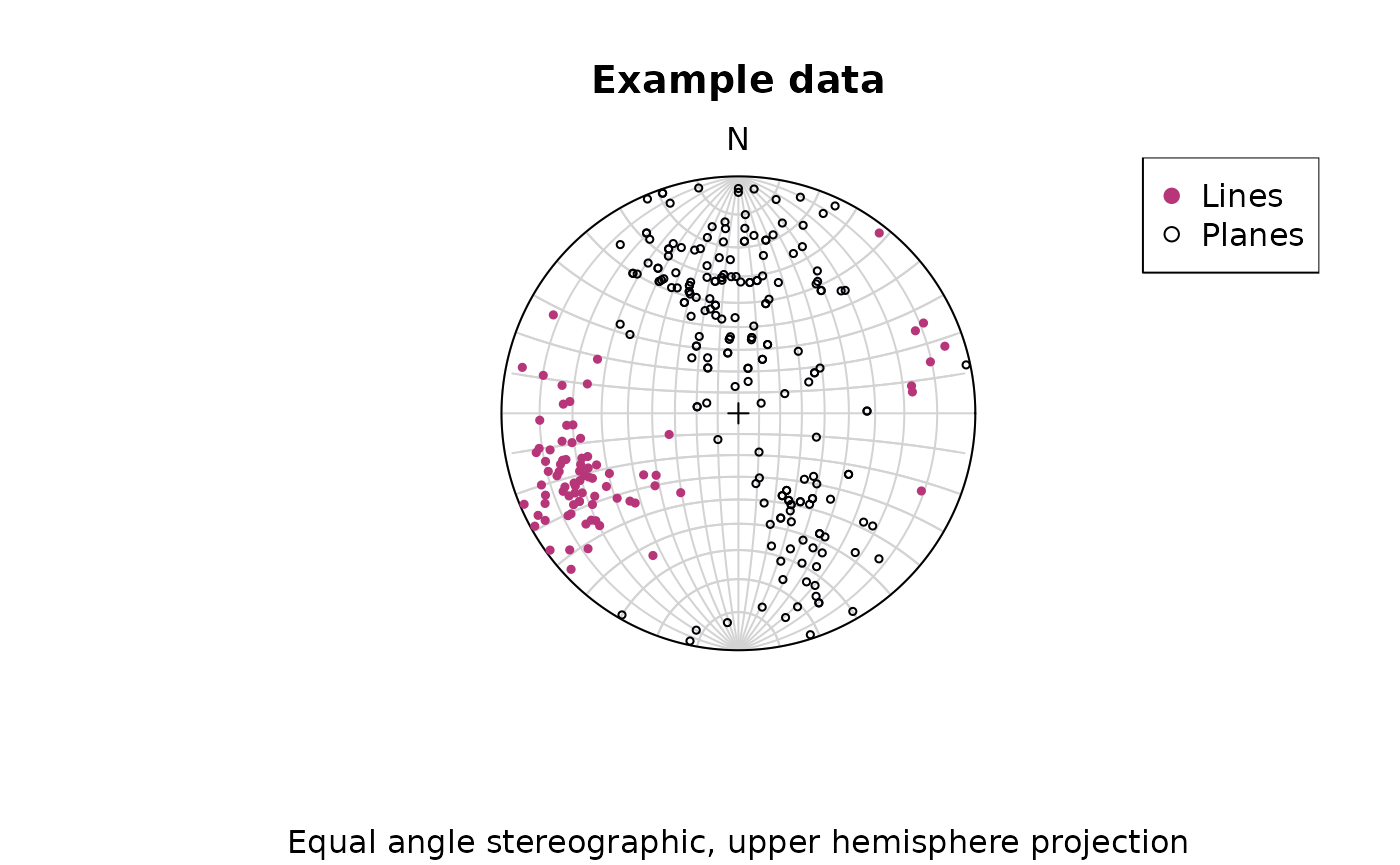

Diagram showing the equal-angle stereographic projection of some example data

Great and small circles

Great and small circles can be added using the lines() function.

Adding great circles:

stereoplot(guides = FALSE) # turn of guides for better visibility
lines(planes, col = "lightgrey", lty = 1)
points(planes, col = "#000004", pch = 1, cex = .5)

Diagram showing greatcircles

To plota small circle with, e.g., a 10° radius, you need to specify the ang argument in lines():

stereoplot(guides = FALSE)
lines(lines[1, ], ang = 10, col = "#B63679", pch = 19, cex = .5)

Diagram showing smallcircles

Fabric plots

The Eigenvalues of the orientation tensor describe the shape of the distribution of these vectors, that is who clustered, cylindrical or random these vectors are distributed.

A Fabric plot visualizes the shape of the distribution by plotting the eigenvalues of the orientation tensor. Three different diagram are provided by {structr}, namely the triangular Vollmer plot after Vollmer (1990), the logarithmic biplot (Woodcock plot) after Woodcock (1977), and the Lode parameter vs. natural octahedral strain diagram (Hsü plot) after Hsü (1965).

Vollmer plot

vollmer_plot() creates a triangular plot showing the shape of the orientation distribution (after Vollmer, 1990).

vollmer_plot(planes, col = "#000004", pch = 1, cex = 2)
vollmer_plot(lines, add = TRUE, col = "#B63679", pch = 19, cex = 2)
legend("topright", legend = c("Lines", "Planes"), col = c("#B63679", "#000004"), pch = c(19, 1), cex = 1)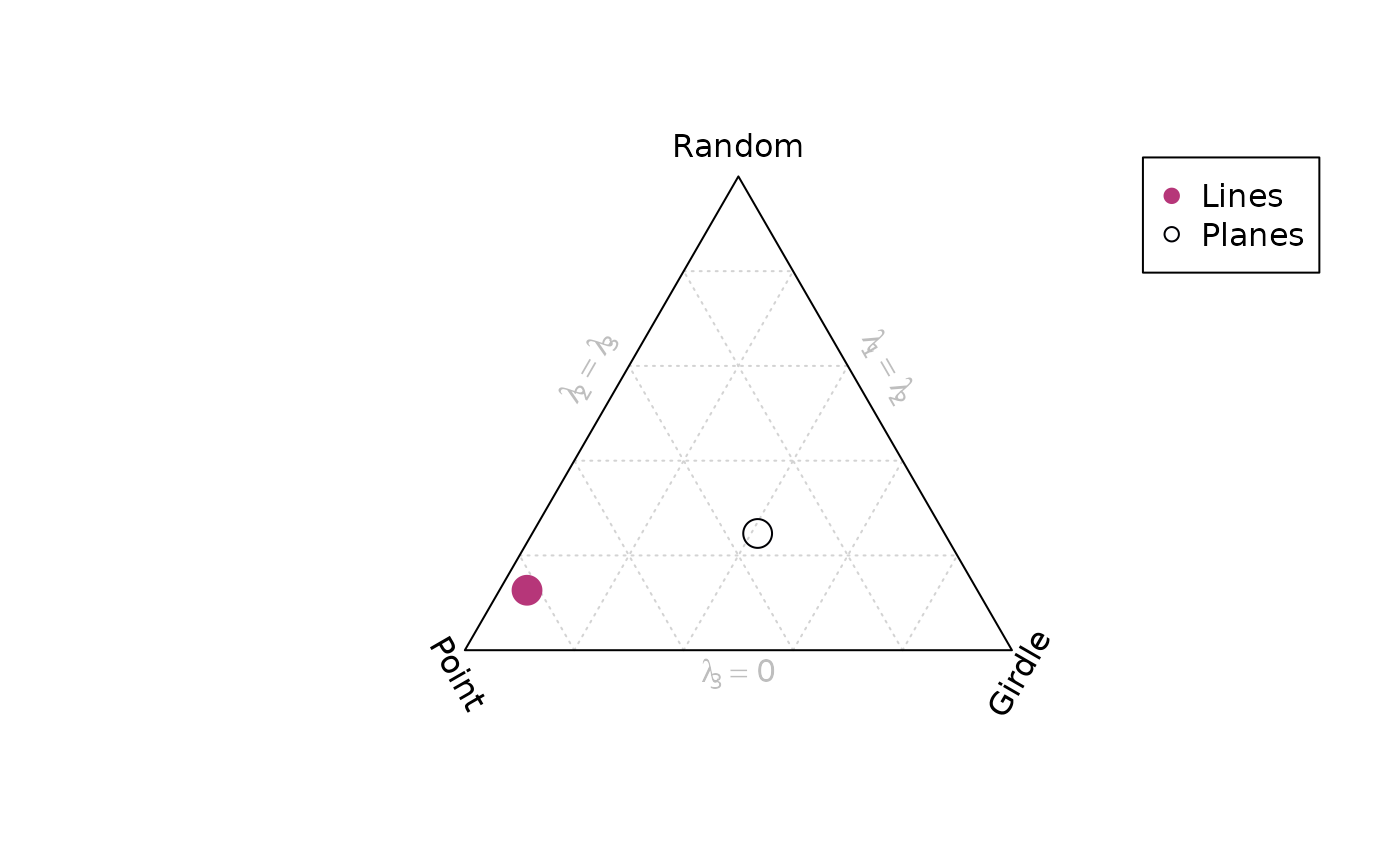

Diagram showing eigen-vector analysis of some example data plotted in an triangular plot after Vollmer 1990

Woodcock plot

woodcock_plot() creates a logarithmic biplot showing the shape of the orientation distribution (after Woodcock, 1977).

woodcock_plot(planes, col = "#000004", pch = 1, cex = 2)
woodcock_plot(lines, add = TRUE, col = "#B63679", pch = 19, cex = 2)
legend("topright", legend = c("Lines", "Planes"), col = c("#B63679", "#000004"), pch = c(19, 1), cex = 1)

Diagram showing eigen-vector analysis of some example data plotted in an biplot plot after Woodcok 1977

Hsü plot

hsu_fabric_plot() creates a Lode parameter vs. natural octahedral strain diagram showing the shape of the orientation distribution (after Hsü, 1965).

hsu_fabric_plot(planes, col = "#000004", pch = 1, cex = 2)
hsu_fabric_plot(lines, add = TRUE, col = "#B63679", pch = 19, cex = 2)
legend("topright", legend = c("Lines", "Planes"), col = c("#B63679", "#000004"), pch = c(19, 1), cex = 1)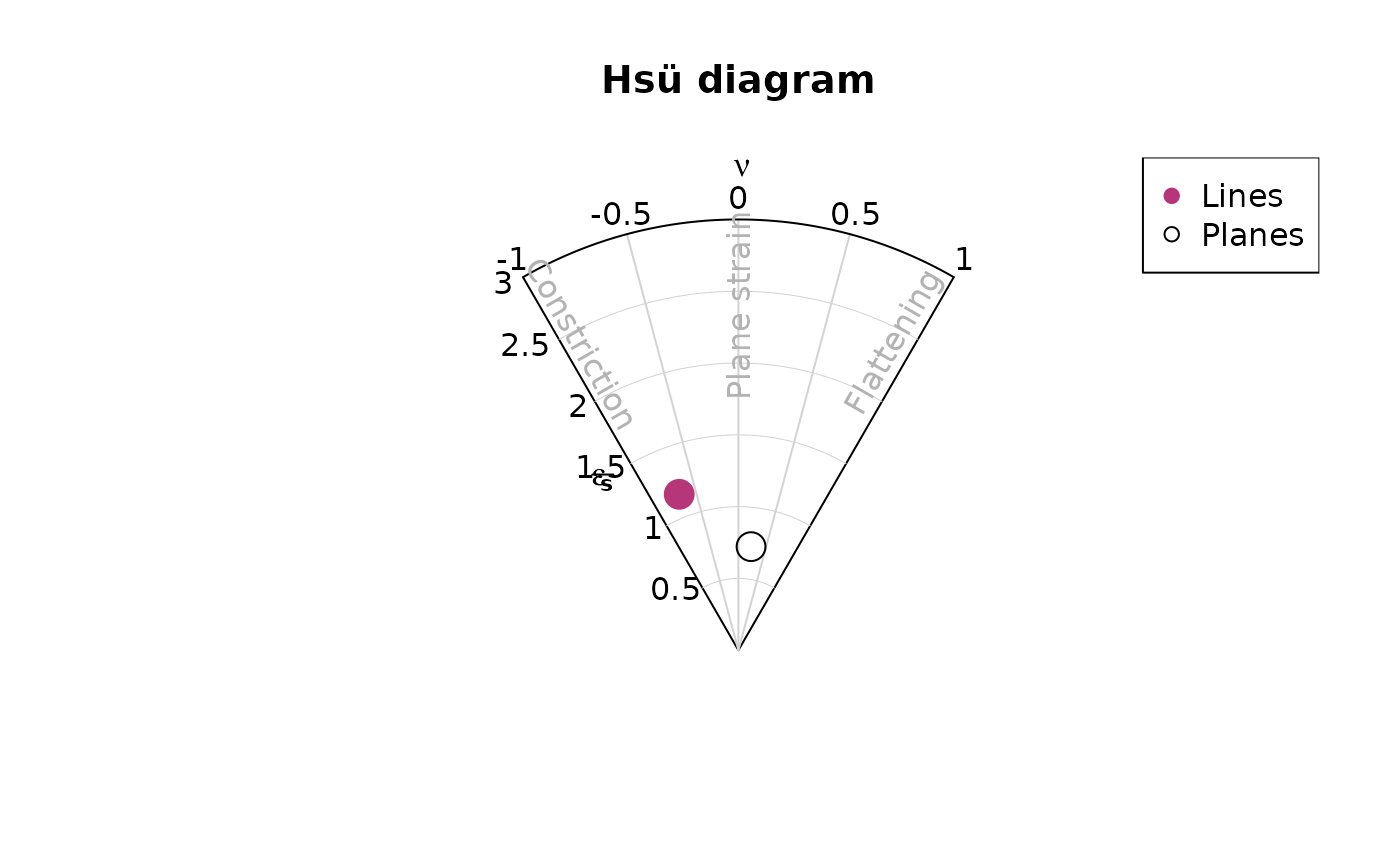

Diagram showing eigen-vector analysis of some example data plotted in a Hsü plot

Density plots

Kamb contours and densities can be added to an existing projection plot using the contour functions. Weighted densities can be controlled by the weights argument and are useful when the orientation measurements have different accuracies.

example_planes_df$quality <- ifelse(is.na(example_planes_df$quality), 6, example_planes_df$quality) # replacing NA values with 6
plane_weightings <- 6 / example_planes_df$quality

stereoplot(guides = FALSE)
points(planes, col = "grey", pch = 16, cex = .5)
contour(planes, add = TRUE, density.params  = list(weights = plane_weightings))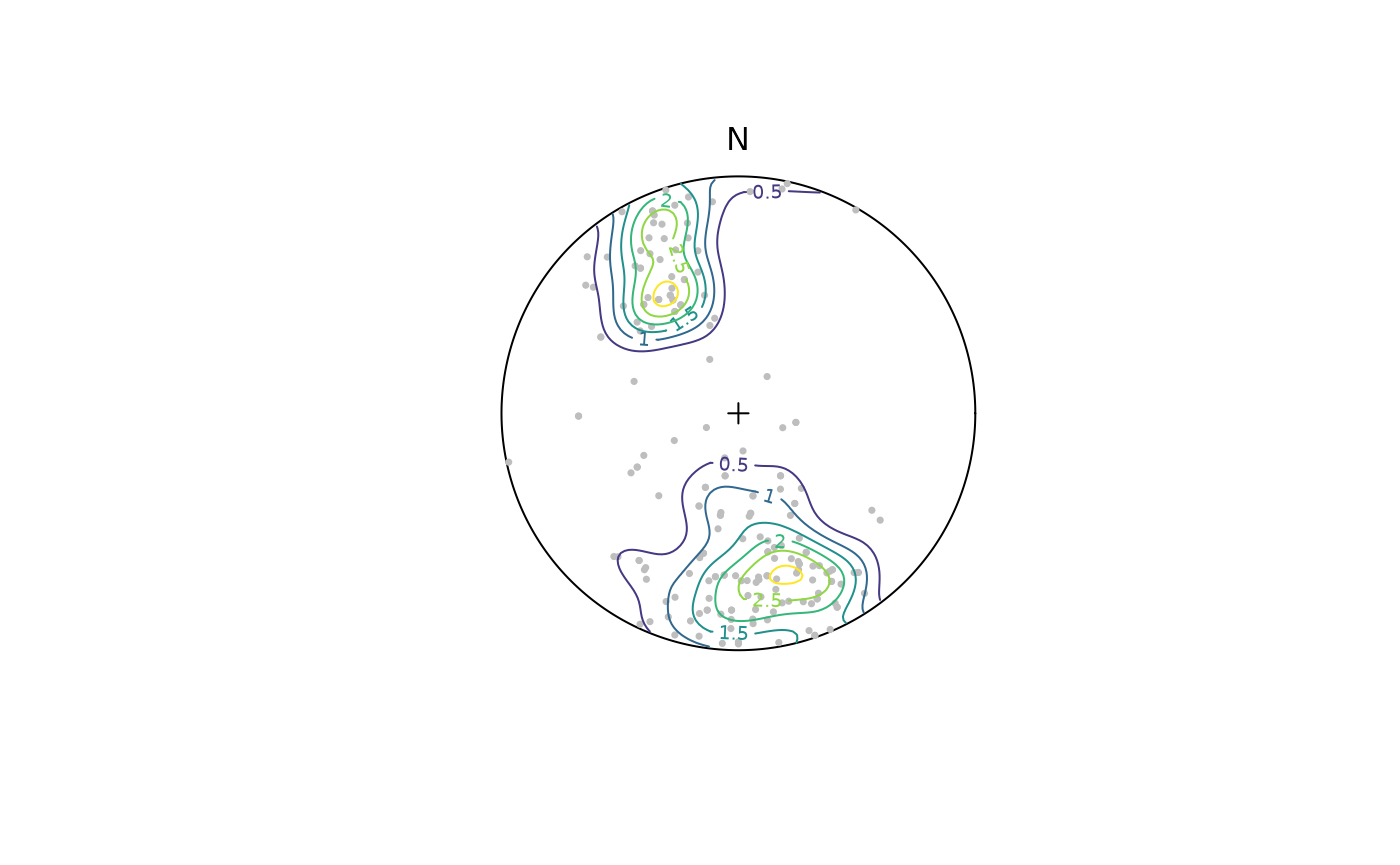

Diagram showing the density distribution some example data plotted in an equal-area projection

contour() adds contour lines, while contourf() adds filled contours and image() adds a density image (i.e. a dense grid of colored rectangles). See ?contour, ?contourf, and ?image for more information.

stereoplot(guides = FALSE)
points(planes, col = "grey", pch = 16, cex = .5)
contourf(planes, add = TRUE, density.params = list(weights = plane_weightings))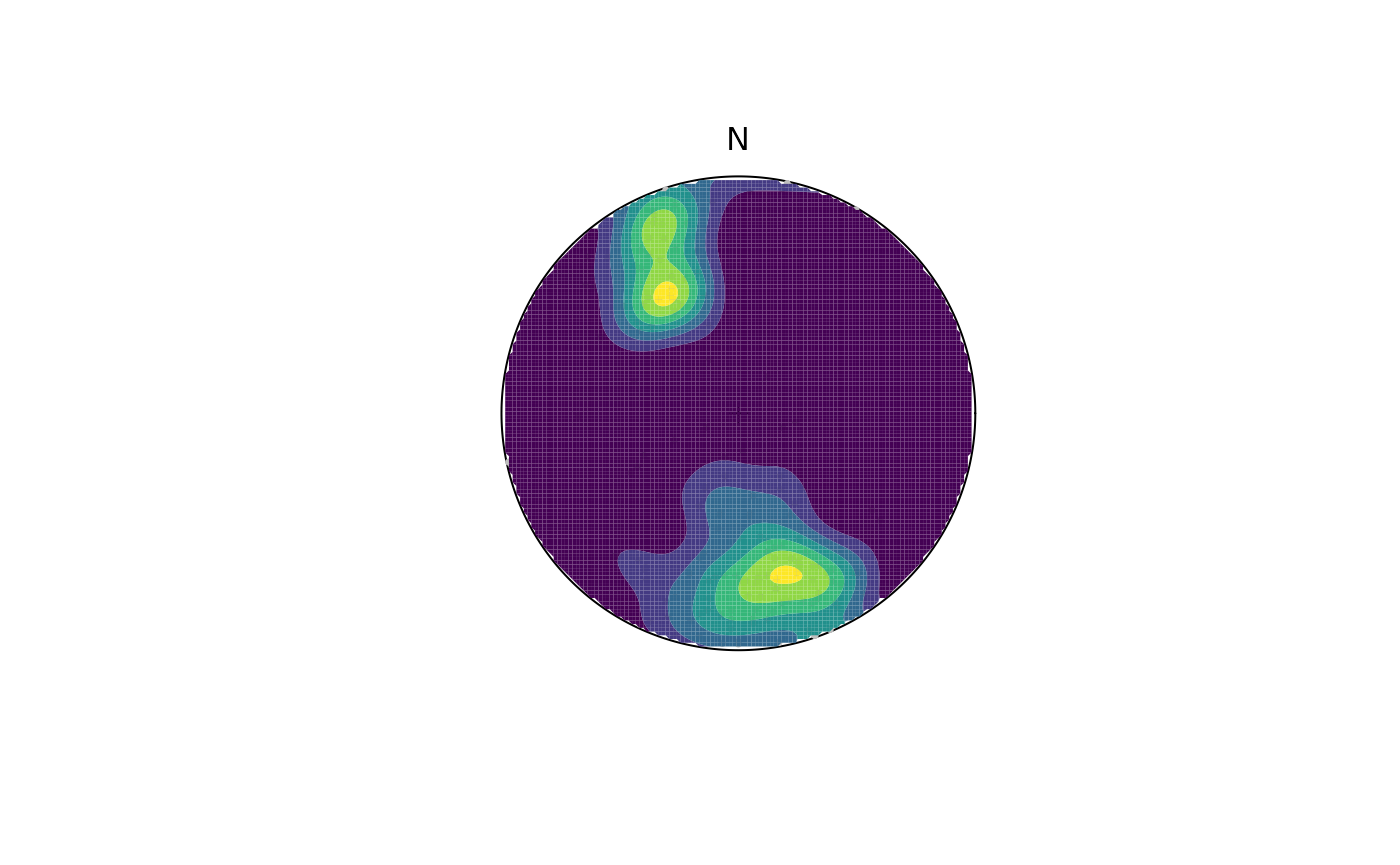

Diagram showing the density distribution some example data plotted in an equal-area projection

Synopsis

Let’s create a publication ready synoptical plot for the line and plane orientation data, showing the density distribution, eigenvectors/mean values, and fabric strength.

# Minimum eigenvector of plane's orientation tensor:
planes_eigen <- ot_eigen(planes)$vectors
planes_eigen3 <- planes_eigen[3, ]

# Mean and SD of lines
lines_mean <- sph_mean(lines)
lines_sd <- sph_sd(lines)

# Fabric strength
fabric_p <- or_shape_params(planes)$Vollmer["D"]
fabric_l <- or_shape_params(lines)$Vollmer["D"]

The final plot:

# two plots side by side
par(mfrow = c(1, 2))

# Planes
stereoplot(guides = TRUE, col = "grey96")
points(planes, col = "grey", pch = 16, cex = .5)
contour(planes, add = TRUE, weights = plane_weightings)
points(planes_eigen3, col = "black", pch = 16)
lines(planes_eigen3, col = "black", pch = 16)
title(
  main = "Planes",
  sub = paste0(
    "N: ", nrow(planes), " | Fabric strength: ", round(fabric_p, 2),
    "\nLambert equal area, lower hemisphere projection"
  )
)

# Lines
stereoplot(guides = TRUE, col = "grey96")
points(lines, col = "grey", pch = 16, cex = .5)
contour(lines, add = TRUE, weights = line_weightings)
points(lines_mean, col = "black", pch = 16)
lines(lines_mean, ang = lines_sd,  col = "black")
title(
  main = "Lines",
  sub = paste0(
    "N: ", nrow(lines), " | Fabric strength: ", round(fabric_l, 2),
    "\nLambert equal area, lower hemisphere projection"
  )
)

Diagram showing the density distribution, eigenvectors and mean values

Fault plots

Fault objects consist of planes (fault plane), lines (e.g. striae), and the sense of movement. There are two ways how these combined features can be visualized, namely the Angelier and the Hoeppner plot.

Angelier plot

The Angelier plot shows all planes as great circles and lineations as points (after Angelier , 1984). Fault striae are plotted as vectors on top of the lineation pointing in the movement direction of the hanging wall. Easy to read in case of homogeneous or small datasets.

f <- Fault(
  c("a" = 120, "b" = 125, "c" = 100),
  c(60, 62, 50),
  c(110, 25, 30),
  c(58, 9, 23),
  c(1, -1, 1)
)

stereoplot(title = "Angelier plot")
angelier(f, col = viridis::magma(nrow(f), end = .9))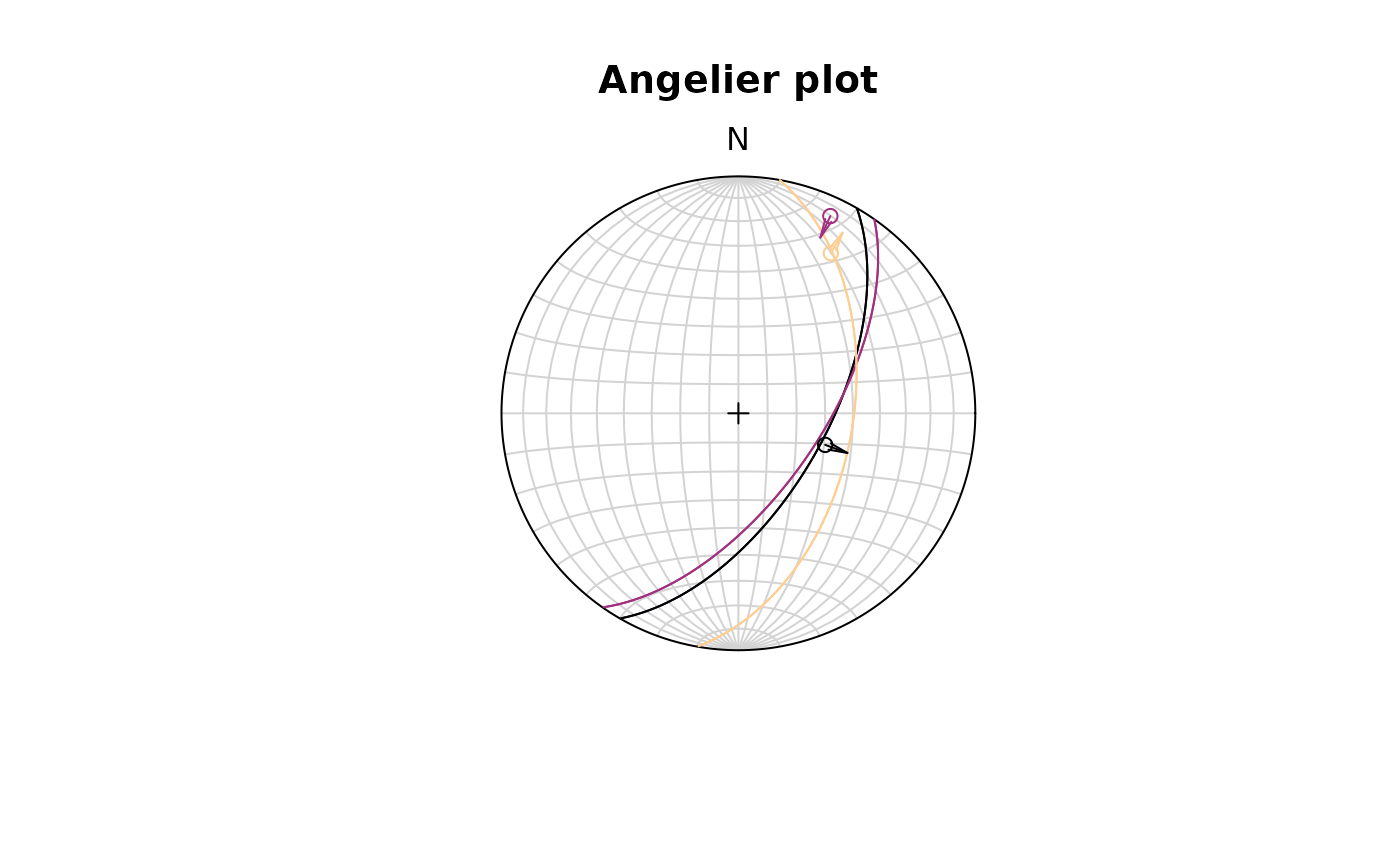

Diagram showing example fault data plotted in an equal-area projection

Hoeppner plot

The Hoeppner plot shows all planes as poles while lineations are not shown (after Hoeppner, 1955). Instead, fault striae are plotted as vectors on top of poles pointing in the movement direction of the hanging wall. Useful in case of large or heterogeneous datasets.

stereoplot(title = "Hoeppner plot")
hoeppner(f, col = viridis::magma(nrow(f), end = .9), points = FALSE)