Stress Inversion for Fault-Slip Data

Determines the orientation of the principal stresses from fault slip data using the Michael (1984) method. Confidence intervals are estimated by bootstrapping. This inversion is simplified by the assumption that the magnitude of the tangential traction on the various fault planes, at the time of rupture, is similar.

Usage

slip_inversion(x, boot = 100L, conf.level = 0.95, ...)

slip_inversion(x, boot = 100L, conf.level = 0.95, ...)

Arguments

x: "Fault" object
boot: integer. Number of bootstrap samples (10 by default)
conf.level: numeric. Confidence level of the interval (0.95 by default)
...: optional parameters passed to confidence_ellipse()

Value

list

stress_tensor: matrix. Best-fit devitoric stress tensor
principal_axes: "Line" obects. Orientation of the principal stress axes
principal_axes_conf: list containg the confidence ellipses for the 3 principal stress vectors. See confidence_ellipse() for details.
principal_vals: numeric. The proportional magnitudes of the principal stress axes given by the eigenvalues of the stress tensor: \(\sigma_1\), \(\sigma_2\), and \(\sigma_3\)
principal_vals_conf: 3-colum vector containing the lower and upper margins of the confidence interval of the principal vals
R: numeric. Stress shape ratio after Gephart & Forsyth (1984): \(R = (\sigma_1 - \sigma_2)/(\sigma_1 - \sigma_3)\). Values ranging from 0 to 1, with 0 being \(\sigma_1 = \sigma_2\) and 1 being \(\sigma_2 = \sigma_3\).
R_conf: Confidence interval for R
phi: numeric. Stress shape ratio after Angelier (1979): \(\Phi = (\sigma_2 - \sigma_3)/(\sigma_1 - \sigma_3)\). Values range between 0 (\(\sigma_2 = \sigma_3\)) and 1 (\(\sigma_2 = \sigma_1\)).
phi_conf: Confidence interval for phi
bott: numeric. Stress shape ratio after Bott (1959): \(\R = (\sigma_3 - \sigma_1)/(\sigma_2 - \sigma_1)\). Values range between \(-\infty\) and \(+\infty\).
bott_conf: Confidence interval for bott
beta: numeric. Average angle between the tangential traction predicted by the best stress tensor and the slip vector on each plane. Should be close to 0.
sigma_s: numeric. Average resolved shear stress on each plane. Should be close to 1.
fault_data: data.frame containing the beta angles, the angles between sigma 1 and the plane normal, the resolved shear and normal stresses, and the slip and dilation tendency on each plane.

list

stress_tensor: matrix. Best-fit devitoric stress tensor
principal_axes: "Line" obects. Orientation of the principal stress axes
principal_axes_conf: list containg the confidence ellipses for the 3 principal stress vectors. See confidence_ellipse() for details.
principal_vals: numeric. The proportional magnitudes of the principal stress axes given by the eigenvalues of the stress tensor: \(\sigma_1\), \(\sigma_2\), and \(\sigma_3\)
principal_vals_conf: 3-colum vector containing the lower and upper margins of the confidence interval of the principal vals
R: numeric. Stress shape ratio after Gephart & Forsyth (1984): \(R = (\sigma_1 - \sigma_2)/(\sigma_1 - \sigma_3)\). Values ranging from 0 to 1, with 0 being \(\sigma_1 = \sigma_2\) and 1 being \(\sigma_2 = \sigma_3\).
R_conf: Confidence interval for R
phi: numeric. Stress shape ratio after Angelier (1979): \(\Phi = (\sigma_2 - \sigma_3)/(\sigma_1 - \sigma_3)\). Values range between 0 (\(\sigma_2 = \sigma_3\)) and 1 (\(\sigma_2 = \sigma_1\)).
phi_conf: Confidence interval for phi
bott: numeric. Stress shape ratio after Bott (1959): \(\R = (\sigma_3 - \sigma_1)/(\sigma_2 - \sigma_1)\). Values range between \(-\infty\) and \(+\infty\).
bott_conf: Confidence interval for bott
beta: numeric. Average angle between the tangential traction predicted by the best stress tensor and the slip vector on each plane. Should be close to 0.
beta_CI: numeric. Confidence interval of beta angle
sigma_s: numeric. Average resolved shear stress on each plane. Should be close to 1.
fault_data: data.frame containing the beta angles, the angles between sigma 1 and the plane normal, the resolved shear and normal stresses, and the slip and dilation tendency on each plane.

Details

The goal of slip inversion is to find the single uniform stress tensor that most likely caused the faulting events. With only slip data to constrain the stress tensor the isotropic component can not be determined, unless assumptions about the fracture criterion are made. Hence inversion will be for the deviatoric stress tensor only. A single fault can not completely constrain the deviatoric stress tensor a, therefore it is necessary to simultaneously solve for a number of faults, so that a single a that best satisfies all of the faults is found.

References

Michael, A. J. (1984). Determination of stress from slip data: Faults and folds. Journal of Geophysical Research: Solid Earth, 89(B13), 11517–11526. https://doi.org/10.1029/JB089iB13p11517

Examples

# Use Angelier examples:
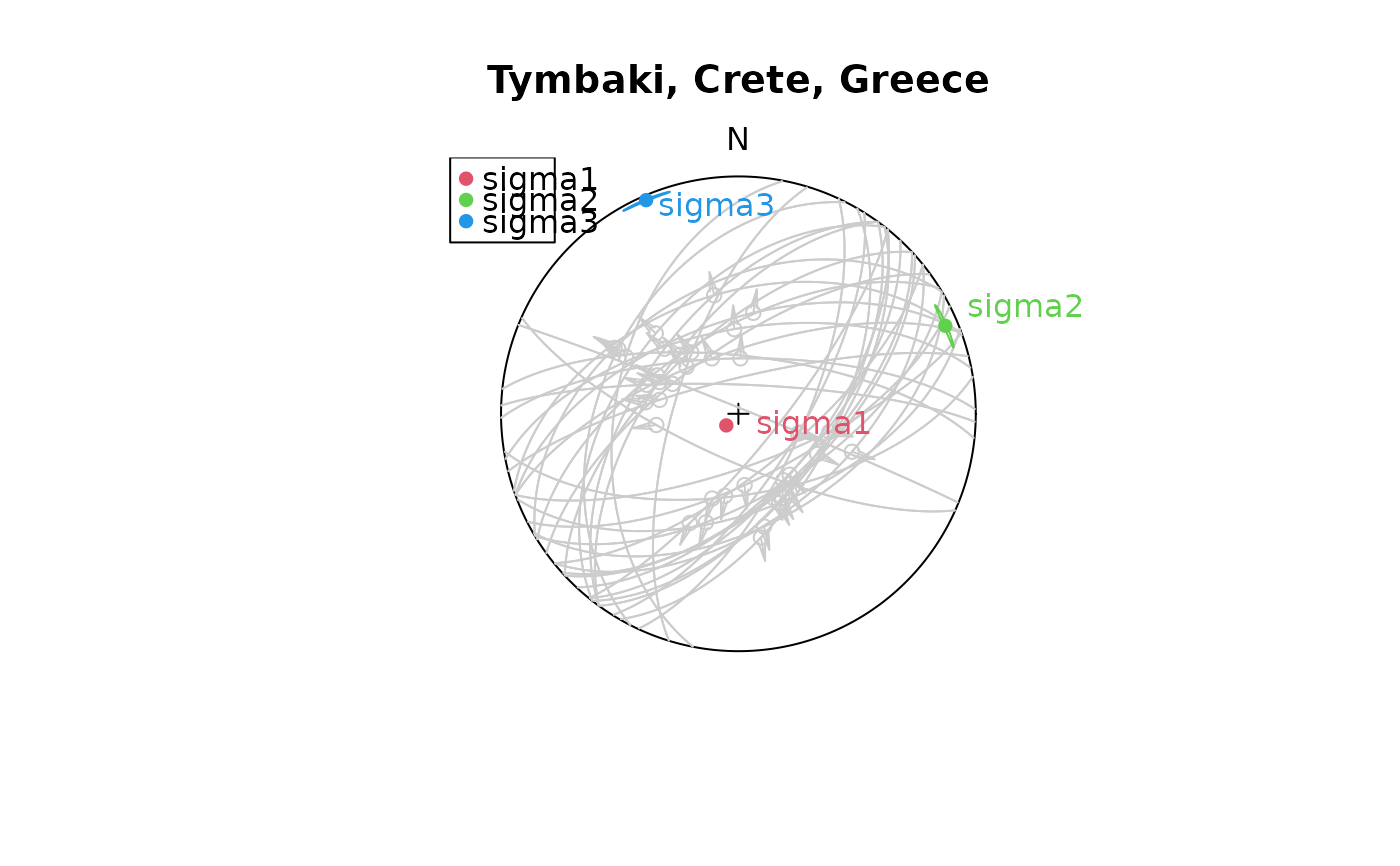
res_TYM <- slip_inversion(angelier1990$TYM, boot = 10)

# Plot the faults (color-coded by beta angle) and show the principal stress axes
stereoplot(title = "Tymbaki, Crete, Greece", guides = FALSE)
fault_plot(angelier1990$TYM, col = "gray80")
stereo_confidence(res_TYM$principal_axes_conf$sigma1, col = 2)
stereo_confidence(res_TYM$principal_axes_conf$sigma2, col = 3)
stereo_confidence(res_TYM$principal_axes_conf$sigma3, col = 4)
text(res_TYM$principal_axes, label = rownames(res_TYM$principal_axes), col = 2:4, adj = -.25)
legend("topleft", col = 2:4, legend = rownames(res_TYM$principal_axes), pch = 16)


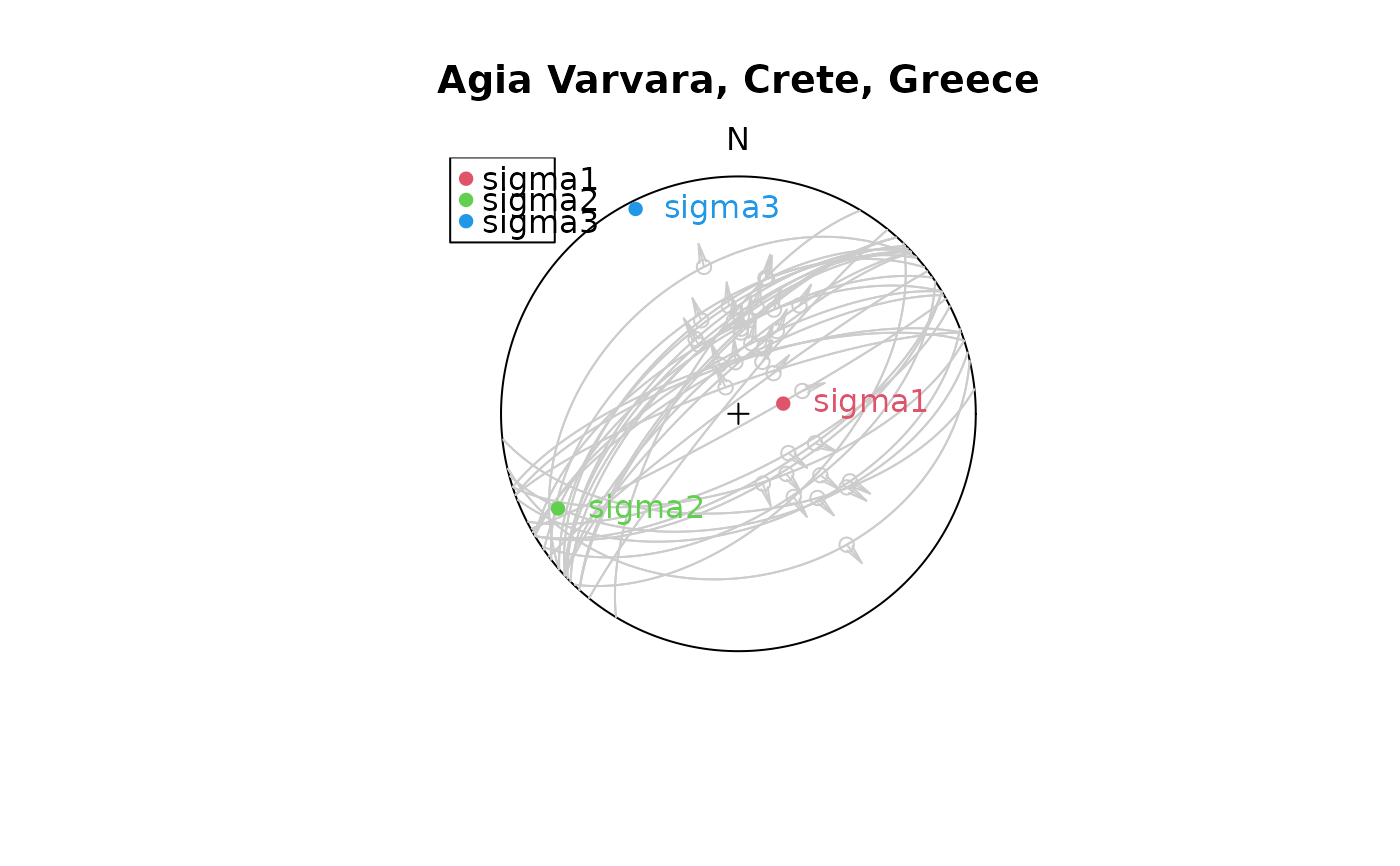
res_AVB <- slip_inversion(angelier1990$AVB)
stereoplot(title = "Agia Varvara, Crete, Greece", guides = FALSE)
fault_plot(angelier1990$AVB, col = "gray80")
stereo_confidence(res_AVB$principal_axes_conf$sigma1, col = 2)
stereo_confidence(res_AVB$principal_axes_conf$sigma2, col = 3)
stereo_confidence(res_AVB$principal_axes_conf$sigma3, col = 4)
text(res_AVB$principal_axes, label = rownames(res_AVB$principal_axes), col = 2:4, adj = -.25)
legend("topleft", col = 2:4, legend = rownames(res_AVB$principal_axes), pch = 16)

set.seed(20250411)
# Use Angelier examples:
res_TYM <- slip_inversion(angelier1990$TYM, boot = 100, n = 1000, res = 100)

# Plot the faults (color-coded by beta angle) and show the principal stress axes
stereoplot(title = "Tymbaki, Crete, Greece", guides = FALSE)
fault_plot(angelier1990$TYM, col = "gray80")
stereo_confidence(res_TYM$principal_axes_conf$sigma1, col = 2)
stereo_confidence(res_TYM$principal_axes_conf$sigma2, col = 3)
stereo_confidence(res_TYM$principal_axes_conf$sigma3, col = 4)
text(res_TYM$principal_axes, label = rownames(res_TYM$principal_axes), col = 2:4, adj = -.25)
legend("topleft", col = 2:4, legend = rownames(res_TYM$principal_axes), pch = 16)


res_AVB <- slip_inversion(angelier1990$AVB, boot = 100, n = 1000, res = 100)
stereoplot(title = "Agia Varvara, Crete, Greece", guides = FALSE)
fault_plot(angelier1990$AVB, col = "gray80")
stereo_confidence(res_AVB$principal_axes_conf$sigma1, col = 2)
stereo_confidence(res_AVB$principal_axes_conf$sigma2, col = 3)
stereo_confidence(res_AVB$principal_axes_conf$sigma3, col = 4)
text(res_AVB$principal_axes, label = rownames(res_AVB$principal_axes), col = 2:4, adj = -.25)
legend("topleft", col = 2:4, legend = rownames(res_AVB$principal_axes), pch = 16)