5. Spatial interpolation

Tobias Stephan

2024-11-12

This vignette teaches you how to spatially interpolate stress fields and display the lateral patterns of stress anomalies.

library(tectonicr)
library(ggplot2) # load ggplot library

data("san_andreas")

data("cpm_models")
por <- cpm_models |>
  subset(model == "NNR-MORVEL56") |>
  equivalent_rotation("na", "pa")

Interpolation

Geographic coordinate system

Spatial interpolation of stress data is based on the aforementioned metrics:

mean_SH <- stress2grid(san_andreas, gridsize = 1, R_range = seq(50, 350, 100))

The default settings apply quality and inverse distance weighting of the mean, as well as a 25% cut-off for the standard deviation.

The tectonicr algorithm is a modified version of the MATLAB algorithm ‘stress2grid’ by Ziegler and Heidbach (2017) but it is faster and provides additional features. See help(stress2grid) for more details and settings, such as different statistics for calculating the orientation average, adjustments of the weighting power of the distance, quality or method.

The data can now be visualized:

trajectories <- eulerpole_loxodromes(x = por, n = 40, cw = FALSE)

ggplot(mean_SH) +
  geom_sf(data = trajectories, lty = 2) +
  geom_spoke(data = san_andreas, aes(lon, lat, angle = deg2rad(90 - azi)), radius = .5, color = "grey30", position = "center_spoke") +
  geom_spoke(aes(lon, lat, angle = deg2rad(90 - azi), alpha = sd, color = mdr), radius = 1, position = "center_spoke", lwd = 1) +
  coord_sf(xlim = range(san_andreas$lon), ylim = range(san_andreas$lat)) +
  scale_alpha(name = "Standard deviation", range = c(1, .25)) +
  scale_color_viridis_c(
    "Wavelength\n(R-normalized mean distance)",
    limits = c(0, 1),
    breaks = seq(0, 1, .25)
  ) +
  facet_wrap(~R)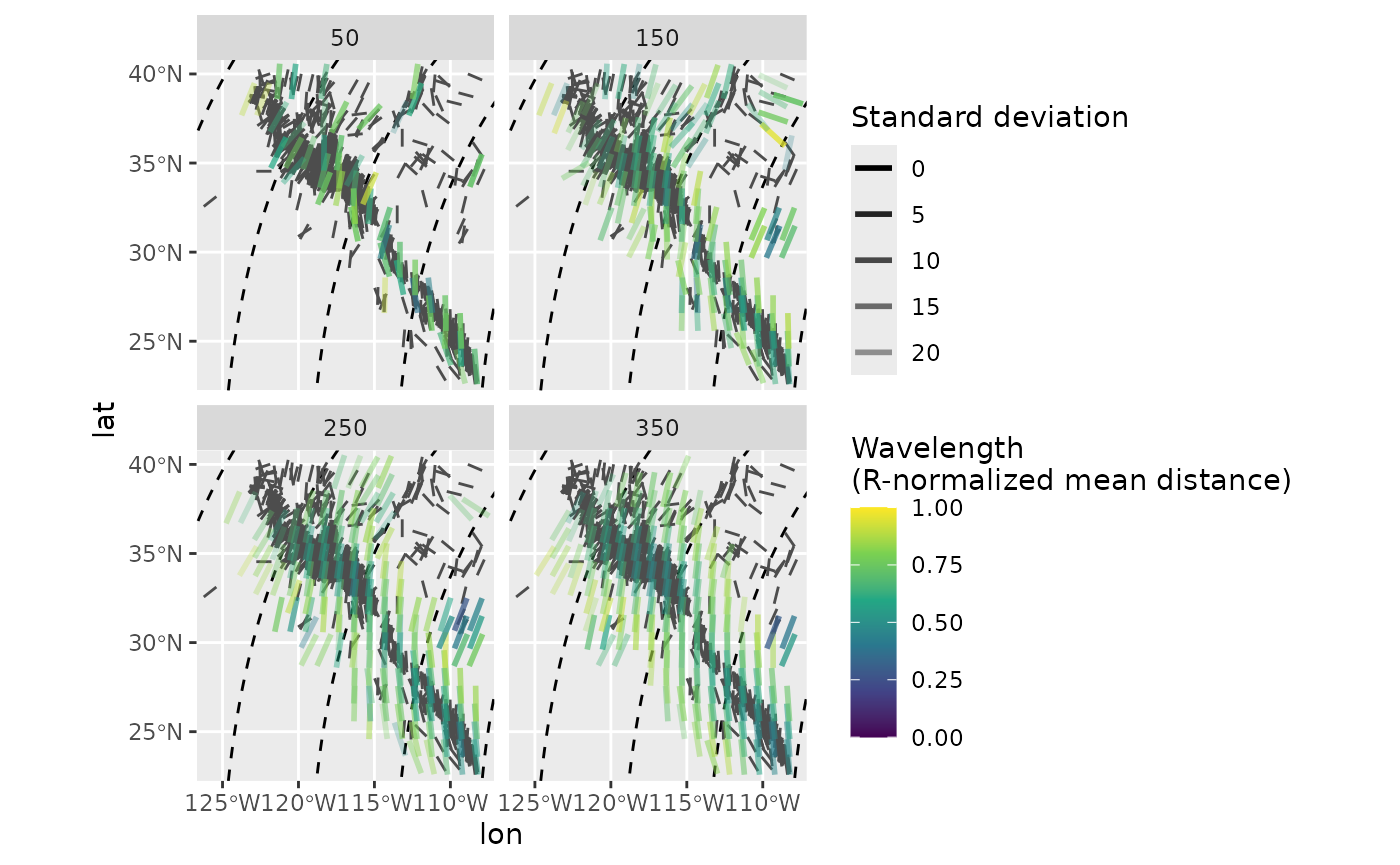

PoR coordinate system

The interpolated direction of far apart data points will suffer from distortions due to the underlying projection. In order to prevent such effects, the interpolation can be done in the PoR reference frame where the direction stays constant no matter the distance between the data points. Assuming that the stress field is sourced by the plate boundary force, the model-based interpolation allows more reliable results for areas close to plate boundaries.

mean_SH_PoR <- PoR_stress2grid(san_andreas, PoR = por, gridsize = 1, R_range = seq(50, 350, 100))

ggplot(mean_SH_PoR) +
  geom_sf(data = trajectories, lty = 2) +
  geom_spoke(data = san_andreas, aes(lon, lat, angle = deg2rad(90 - azi)), radius = .5, color = "grey30", position = "center_spoke") +
  geom_spoke(aes(lon, lat, angle = deg2rad(90 - azi), alpha = sd, color = mdr), radius = 1, position = "center_spoke", lwd = 1) +
  coord_sf(xlim = range(san_andreas$lon), ylim = range(san_andreas$lat)) +
  scale_alpha(name = "Standard deviation", range = c(1, .25)) +
  scale_color_viridis_c(
    "Wavelength\n(R-normalized mean distance)",
    limits = c(0, 1),
    breaks = seq(0, 1, .25)
  ) +
  facet_wrap(~R)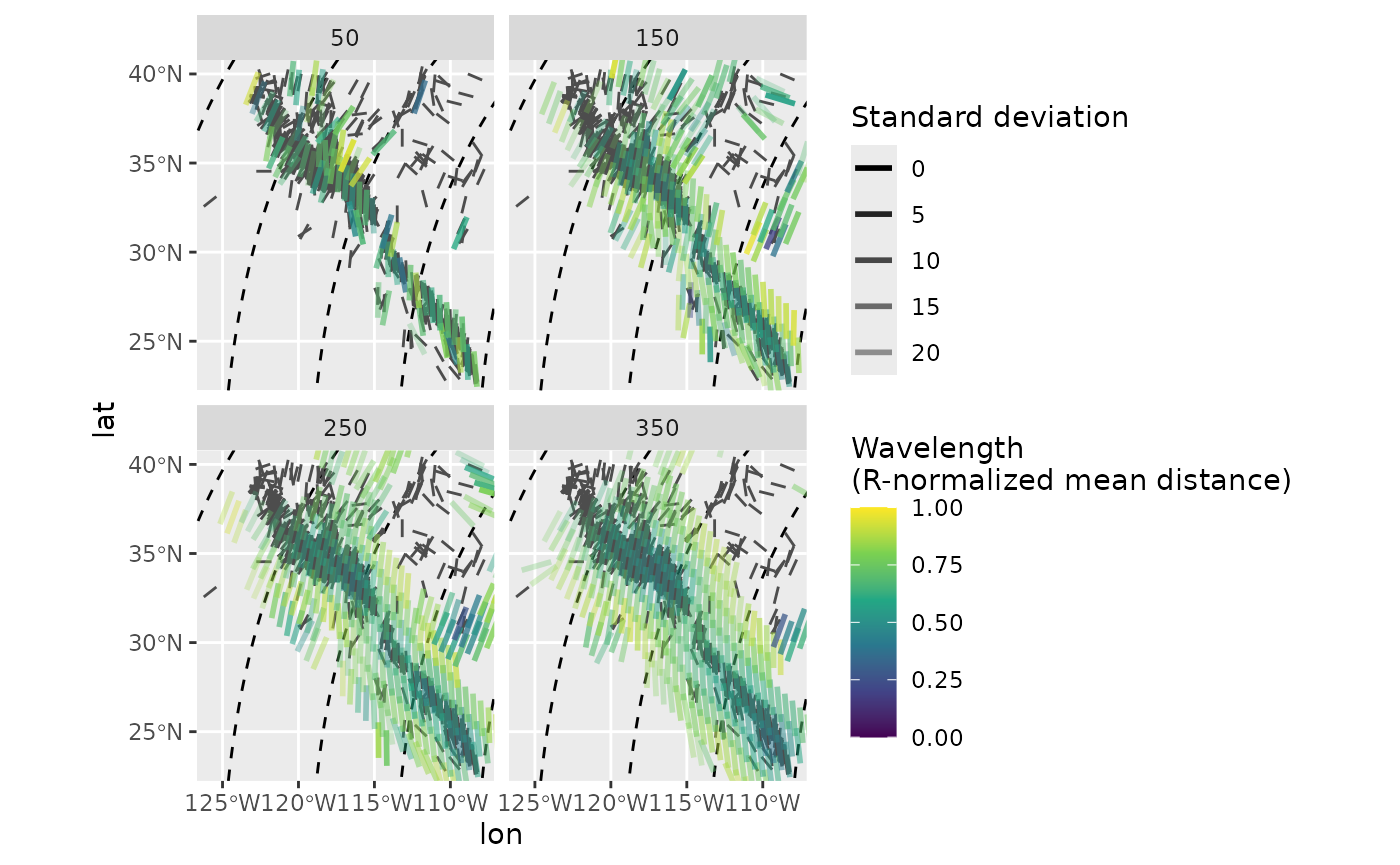

Rasterize the interpolation

The function compact_grid() selects only data with the minimum search radius from interpolated layers with different search radii. Since the interpolation was performed in the PoR CRS, the interpolated azimuths are additionally given in the transformed azimuths. This allows to easily calculate misfits from predicted directions:

mean_SH_PoR_reduced <- mean_SH_PoR |>
  compact_grid() |>
  dplyr::mutate(cdist = circular_distance(azi.PoR, 135))

Using circular_distance() in the example above, we can display the spatial patterns of the misfits of the stress direction from the predicted direction of the plate boundary force. Since the interpolation was performed in the PoR CRS, the grid is not composed of equally spaced grid cells in the geographic CRS. To rasterize such grids, we can, e.g., use Voronoi cells from the ggforce package.

ggplot(mean_SH_PoR_reduced) +
  ggforce::geom_voronoi_tile(
    aes(lon, lat, fill = cdist),
    max.radius = .7, normalize = FALSE
  ) +
  scale_fill_viridis_c("Angular distance", limits = c(0, 1)) +
  geom_sf(data = trajectories, lty = 2) +
  geom_spoke(
    aes(lon, lat, angle = deg2rad(90 - azi), alpha = sd),
    radius = .5, position = "center_spoke", lwd = .2, colour = "white"
  ) +
  scale_alpha("Standard deviation", range = c(1, .25)) +
  coord_sf(xlim = range(san_andreas$lon), ylim = range(san_andreas$lat))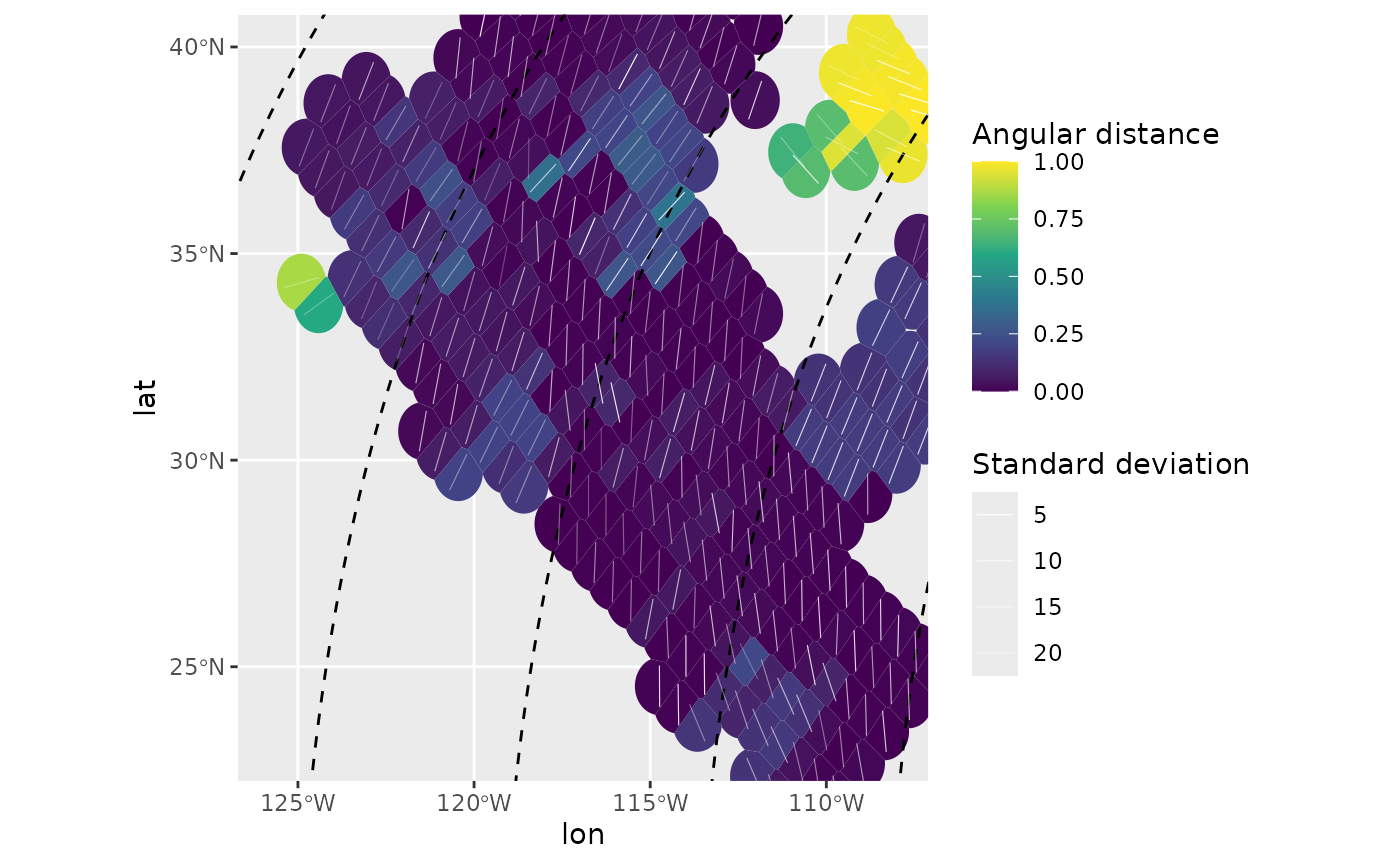

The map highlights stress anomalies which show misfits to the direction of tested plate boundary force.

References

Mardia, K. V., and Jupp, P. E. (Eds.). (1999). “Directional Statistics” Hoboken, NJ, USA: John Wiley & Sons, Inc.  doi: 10.1002/9780470316979.

Ziegler, Moritz O., and Oliver Heidbach. 2017. “Manual of the Matlab Script Stress2Grid” GFZ German Research Centre for Geosciences; World Stress Map Technical Report 17-02. doi: 10.5880/wsm.2017.002.