Decomposition of Orientation Tensor in 2D

Spectral decomposition of the 2D orientation tensor into two Eigenvectors and corresponding Eigenvalues provides provides a measure of location and a corresponding measure of dispersion, respectively.

Usage

ot_eigen2d(x, w = NULL, scale = FALSE)

principal_direction(x, w = NULL)

axial_strength(x, w = NULL)

axial_dispersion(x, w = NULL)

Arguments

x: numeric. Axial angular data (in degrees).
w: (optional) Weights. A vector of positive numbers and of the same length as x.
scale: logical. Whether the Eigenvalues should be scaled so they sum up to 1. Only applicable when weighting are specified, otherwise the eigenvalues are always scaled.

Value

ot_eigen2d returns a list of the Eigenvalues and the axial angles corresponding to the Eigenvectors. principal_direction(), axial_strength() and axial_dispersion() are convenience functions to return the orientation of the largest eigenvalue, the orientation strength, the axial dispersion respectively.

Details

The Eigenvalues (\(\lambda_1 > \lambda_2\)) can be interpreted as the fractions of the variance explained by the orientation of the associated Eigenvectors. The two perpendicular Eigenvectors (\(a_1, a_2\)) are the "principal directions" with respect to the highest and the lowest concentration of orientation data.

The strength of the orientation is the largest eigenvalue \(\lambda_1\) normalized by the sum of the eigenvalues (scale=TRUE). Then \(\lambda_2 = 1-\lambda_1\) is a measure of dispersion of 2D orientation data with respect to \(a_1\).

Note

Eigenvalues and Eigenvectors of the orientation tensor (inertia tensor) are also called "principle moments of inertia" and "principle axes of inertia", respectively.

Examples

test <- rvm(100, mean = 0, k = 10) / 2
ot_eigen2d(test)
#> eigen() decomposition
#> $values
#> [1] 0.97486598 0.02513402
#> 
#> $vectors
#> [1]   1.822026 -88.177974
#> 

data("nuvel1")
PoR <- subset(nuvel1, nuvel1$plate.rot == "na")
sa.por <- PoR_shmax(san_andreas, PoR, "right")
sa_eig <- ot_eigen2d(sa.por$azi.PoR, w = weighting(san_andreas$unc), scale = TRUE)
print(sa_eig)
#> eigen() decomposition
#> $values
#> [1] 0.8750106 0.1249894
#> 
#> $vectors
#> [1] -39.20782  50.79218
#> 

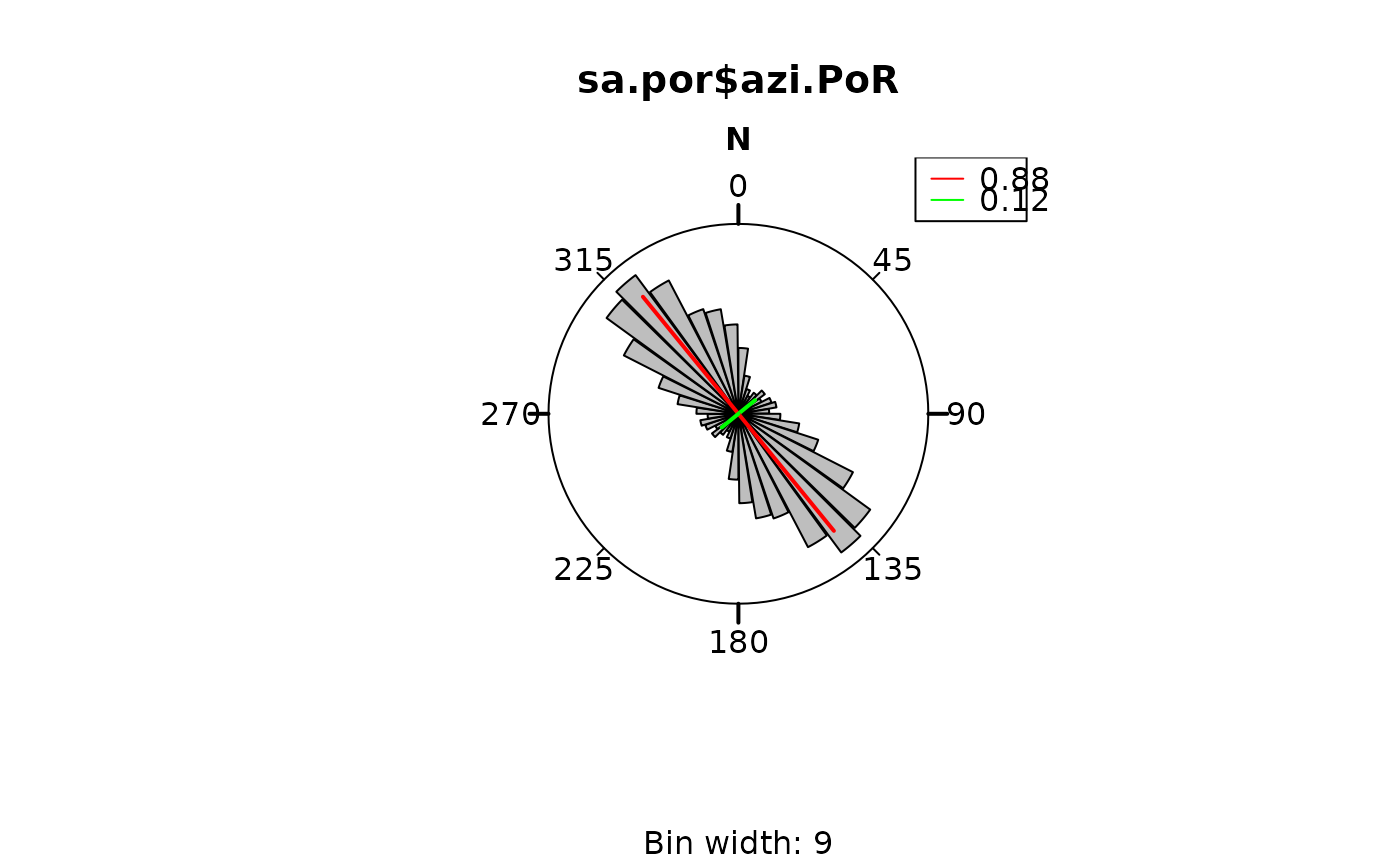
rose(sa.por$azi.PoR, muci = FALSE)
rose_line(sa_eig$vectors,
  col = c("red", "green"),
  radius = sa_eig$values, lwd = 2
)
graphics::legend("topright",
  legend = round(sa_eig$values, 2),
  col = c("red", "green"), lty = 1
)


principal_direction(sa.por$azi.PoR)
#> [1] -39.12223

axial_strength(sa.por$azi.PoR)
#> [1] 0.8579857

axial_dispersion(sa.por$azi.PoR)
#> [1] 0.1420143